- Равномерное прямолинейное движение. Закон движения тела, движущегося равномерно прямолинейно
- знать понятие «равномерное прямолинейное движение»; общий вид уравнения координаты тела, движущегося равномерно прямолинейно; графики зависимости координаты от времени и скорости от времени при равномерном прямолинейном движении
- уметь записывать закон движения тела, движущегося равномерно прямолинейно
- Какое движение называется равномерным?
- Как вычислить скорость при равномерном прямолинейном движении?
- Как выглядит график скорости тела, движущегося равномерно?
Равномерное прямолинейное движение. Закон движения тела, движущегося равномерно прямолинейно
Если тело движется с постоянной по модулю скоростью и не меняет направления своего движения, говорят, что тело движется равномерно прямолинейно.
Равномерное прямолинейное движение — это движение, при котором вектор скорости не меняется с течением времени.
Пусть автомобиль движется в положительном направлении оси ОХ с постоянной скоростью.
 Рис. 1. Изменение координаты равномерно движущегося тела с течением времени
Рис. 1. Изменение координаты равномерно движущегося тела с течением времени
В момент времени t = 0 тело находится в координате
x0 = 100 м (рис. 1). Через 20 секунд автомобиль оказался в точке с координатой x = 300 м.
Так как за 20 секунд автомобиль проехал 200 метров, его скорость равна = 10 м/с.
Зная, что тело движется равномерно, можно утверждать, что значение начальной координаты x0 автомобиля каждую секунду увеличивается на 10 метров.
Тогда конечную координату в момент времени t будет определять следующая формула:
.
В нашем случае уравнение принимает следующий вид:
.
Данная формула позволяет найти координату автомобиля в любой момент времени и называется законом движения для данного тела.
В общем виде закон движения тела, движущегося равномерно прямолинейно, имеет следующий вид:
,
где x [м] — конечная координата тела;
x0 [м] — начальная координата тела;
[м/с] — проекция скорости тела;
t [с] — время, через которое точечное тело окажется в координате x.
Уравнение (закон) движения определяет координату материальной точки в любой момент времени.
Уравнение движения при прямолинейном равномерном движении имеет следующий вид: .
Если тело движется в направлении, совпадающим с положительным направлением координатной оси, то проекция скорости на данную ось положительна — координата тела будет увеличиваться.
В противном случае, если проекция скорости на координатную ось
отрицательна — координата тела будет уменьшаться.
Понятно, что, подставляя в формулу различные значения времени t, можно найти координату тела в заданный момент времени. Например, рассчитаем координату автомобиля через 2 минуты:
.
При необходимости уравнение можно использовать, чтобы найти промежуток времени, через который тело из точки с координатой x0 переместится в точку с координатой x.
Найдём время, которое понадобится автомобилю, чтобы оказаться в координате
1 500 м. Для этого выразим из формулы время:
.
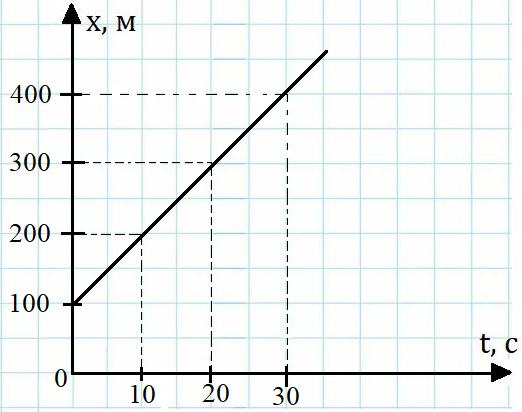 Рис. 2. График зависимости координаты тела от времени при равномерном прямолинейном движении
Рис. 2. График зависимости координаты тела от времени при равномерном прямолинейном движении
Построим график изменения координаты тела, движущегося по закону (рис. 2).
Полученный график зависимости координаты от времени x(t) представляет собой наклонную прямую линию. Аналогично будет выглядеть график движения любого тела, движущегося равномерно прямолинейно, так как зависимость x(t) линейная.
Проанализируем уравнение координаты тела, движущегося равномерно прямолинейно . Понятно, что изменение координаты тела равно разности конечной и начальной координат, тогда справедливо следующее равенство:
.
Из этого соотношения видно, что изменение координаты прямо пропорционально времени движения. Помимо этого, быстрота изменения координаты зависит от скорости движения рассматриваемого тела.
Путь тела, движущегося равномерно прямолинейно, равен модулю изменения координаты тела:
,
где — модуль скорости тела.
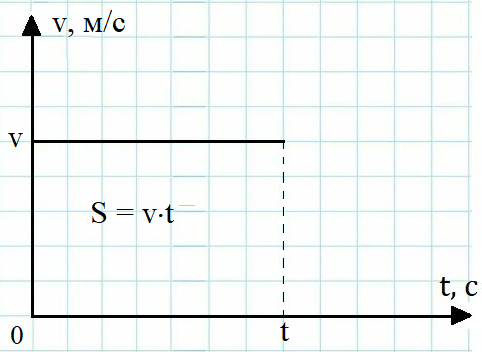 Рис. 3. График скорости равномерно движущегося тела
Рис. 3. График скорости равномерно движущегося тела
Формулу можно получить графически: путь равен площади фигуры под графиком . График скорости равномерно движущегося тела представляет собой прямую линию, параллельную оси абсцисс (рис. 3). Следовательно, фигура под графиком
скорости — это прямоугольник со сторонами и . Получаем, что площадь под графиком скорости равномерно движущегося тела равна произведению .
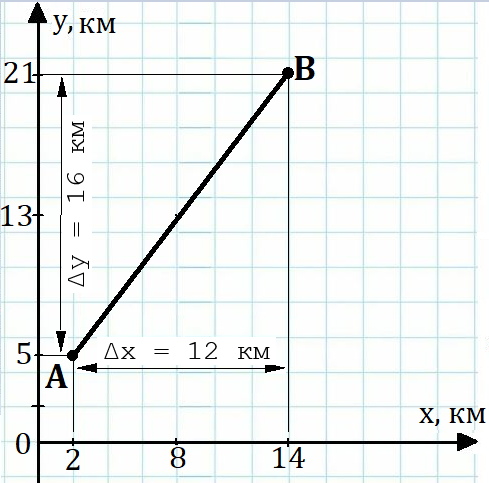 Рис. 4. Траектория движения тела, скорость которого направлена под углом к каждой из координатных осей
Рис. 4. Траектория движения тела, скорость которого направлена под углом к каждой из координатных осей
Рассмотрим движение тела, направление скорости которого не совпадает с направлением ни одной из координатных осей.
Пусть тело движется равномерно прямолинейно из точки А в точку В в плоскости XOY (рис. 4). Время движения равно 2 ч.
В данном случае для описания движения тела необходимо определить законы движения для каждой из координатных осей. Учитывая, что время движения t = 2 ч, проекции скоростей на координатные оси равны:
;
.
Тогда уравнения координат имеют следующий вид:
;
.
Полученные законы движения можно представить в графическом виде — в виде графиков зависимостей x(t) и y(t), представленных на рисунке 5. Количество графиков должно быть равно количеству изменяющихся координат.
 Рис. 5. Графики зависимостей x(t) и y(t)
Рис. 5. Графики зависимостей x(t) и y(t)
Итоги
- Равномерное прямолинейное движение — это движение, при котором вектор скорости не меняется с течением времени.
- Уравнение (закон) движения определяет координату материальной точки в любой момент времени.
- Уравнение движения при прямолинейном равномерном движении имеет следующий вид: .
- Путь тела, движущегося равномерно прямолинейно, равен модулю изменения координаты тела: .
Контрольные вопросы
1. Какое движение называется равномерным прямолинейным?
2. Как выглядит график координаты от времени при равномерном прямолинейном движении?
3. По какому закону изменяется координата тела, движущегося равномерно прямолинейно?
- Равномерное прямолинейное движение. Закон движения тела, движущегося равномерно прямолинейно
- знать понятие «равномерное прямолинейное движение»; общий вид уравнения координаты тела, движущегося равномерно прямолинейно; графики зависимости координаты от времени и скорости от времени при равномерном прямолинейном движении
- уметь записывать закон движения тела, движущегося равномерно прямолинейно
- Какое движение называется равномерным?
- Как вычислить скорость при равномерном прямолинейном движении?
- Как выглядит график скорости тела, движущегося равномерно?
Равномерное прямолинейное движение. Закон движения тела, движущегося равномерно прямолинейно
Если тело движется с постоянной по модулю скоростью и не меняет направления своего движения, говорят, что тело движется равномерно прямолинейно.
Равномерное прямолинейное движение — это движение, при котором вектор скорости не меняется с течением времени.
Пусть автомобиль движется в положительном направлении оси ОХ с постоянной скоростью.
 Рис. 1. Изменение координаты равномерно движущегося тела с течением времени
Рис. 1. Изменение координаты равномерно движущегося тела с течением времени
В момент времени t = 0 тело находится в координате
x0 = 100 м (рис. 1). Через 20 секунд автомобиль оказался в точке с координатой x = 300 м.
Так как за 20 секунд автомобиль проехал 200 метров, его скорость равна = 10 м/с.
Зная, что тело движется равномерно, можно утверждать, что значение начальной координаты x0 автомобиля каждую секунду увеличивается на 10 метров.
Тогда конечную координату в момент времени t будет определять следующая формула:
.
В нашем случае уравнение принимает следующий вид:
.
Данная формула позволяет найти координату автомобиля в любой момент времени и называется законом движения для данного тела.
В общем виде закон движения тела, движущегося равномерно прямолинейно, имеет следующий вид:
,
где x [м] — конечная координата тела;
x0 [м] — начальная координата тела;
[м/с] — проекция скорости тела;
t [с] — время, через которое точечное тело окажется в координате x.
Уравнение (закон) движения определяет координату материальной точки в любой момент времени.
Уравнение движения при прямолинейном равномерном движении имеет следующий вид: .
Если тело движется в направлении, совпадающим с положительным направлением координатной оси, то проекция скорости на данную ось положительна — координата тела будет увеличиваться.
В противном случае, если проекция скорости на координатную ось
отрицательна — координата тела будет уменьшаться.
Понятно, что, подставляя в формулу различные значения времени t, можно найти координату тела в заданный момент времени. Например, рассчитаем координату автомобиля через 2 минуты:
.
При необходимости уравнение можно использовать, чтобы найти промежуток времени, через который тело из точки с координатой x0 переместится в точку с координатой x.
Найдём время, которое понадобится автомобилю, чтобы оказаться в координате
1 500 м. Для этого выразим из формулы время:
.
 Рис. 2. График зависимости координаты тела от времени при равномерном прямолинейном движении
Рис. 2. График зависимости координаты тела от времени при равномерном прямолинейном движении
Построим график изменения координаты тела, движущегося по закону (рис. 2).
Полученный график зависимости координаты от времени x(t) представляет собой наклонную прямую линию. Аналогично будет выглядеть график движения любого тела, движущегося равномерно прямолинейно, так как зависимость x(t) линейная.
Проанализируем уравнение координаты тела, движущегося равномерно прямолинейно . Понятно, что изменение координаты тела равно разности конечной и начальной координат, тогда справедливо следующее равенство:
.
Из этого соотношения видно, что изменение координаты прямо пропорционально времени движения. Помимо этого, быстрота изменения координаты зависит от скорости движения рассматриваемого тела.
Путь тела, движущегося равномерно прямолинейно, равен модулю изменения координаты тела:
,
где — модуль скорости тела.
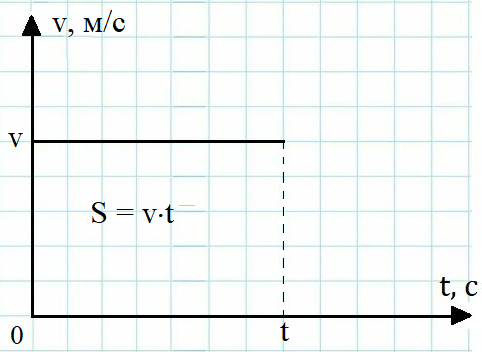 Рис. 3. График скорости равномерно движущегося тела
Рис. 3. График скорости равномерно движущегося тела
Формулу можно получить графически: путь равен площади фигуры под графиком . График скорости равномерно движущегося тела представляет собой прямую линию, параллельную оси абсцисс (рис. 3). Следовательно, фигура под графиком
скорости — это прямоугольник со сторонами и . Получаем, что площадь под графиком скорости равномерно движущегося тела равна произведению .
 Рис. 4. Траектория движения тела, скорость которого направлена под углом к каждой из координатных осей
Рис. 4. Траектория движения тела, скорость которого направлена под углом к каждой из координатных осей
Рассмотрим движение тела, направление скорости которого не совпадает с направлением ни одной из координатных осей.
Пусть тело движется равномерно прямолинейно из точки А в точку В в плоскости XOY (рис. 4). Время движения равно 2 ч.
В данном случае для описания движения тела необходимо определить законы движения для каждой из координатных осей. Учитывая, что время движения t = 2 ч, проекции скоростей на координатные оси равны:
;
.
Тогда уравнения координат имеют следующий вид:
;
.
Полученные законы движения можно представить в графическом виде — в виде графиков зависимостей x(t) и y(t), представленных на рисунке 5. Количество графиков должно быть равно количеству изменяющихся координат.
 Рис. 5. Графики зависимостей x(t) и y(t)
Рис. 5. Графики зависимостей x(t) и y(t)
Итоги
- Равномерное прямолинейное движение — это движение, при котором вектор скорости не меняется с течением времени.
- Уравнение (закон) движения определяет координату материальной точки в любой момент времени.
- Уравнение движения при прямолинейном равномерном движении имеет следующий вид: .
- Путь тела, движущегося равномерно прямолинейно, равен модулю изменения координаты тела: .
Контрольные вопросы
1. Какое движение называется равномерным прямолинейным?
2. Как выглядит график координаты от времени при равномерном прямолинейном движении?
3. По какому закону изменяется координата тела, движущегося равномерно прямолинейно?



