- Повторение определения и основных формул геометрической прогрессии
- Введение бесконечно убывающей геометрической прогрессии и ее суммы
- Вычисление суммы бесконечно убывающей геометрической прогрессии
- Запись периодической десятичной дроби в виде обыкновенной с использованием суммы бесконечно убывающей геометрической прогрессии
- Знать, какая прогрессия будет геометрической, бесконечно убывающей геометрической, формулу суммы бесконечно убывающей геометрической прогрессии
- Уметь применять знания на практике
Вспомним определение и основные формулы для геометрической прогрессии.
Геометрическая прогрессия – такая числовая последовательность , что для всех натуральных n выполняется равенство
Формула n-го члена геометрической прогрессии:
(1)
Формула суммы первых n членов геометрической прогрессии:
(2)
- Продолжите фразу «бесконечная непериодическая десятичная дробь называется…». Приведите пример.
- Представьте число в виде периодической дроби.
- Вычислить сумму первых пяти членов геометрической прогрессии, если
Рассмотрим равносторонний треугольник со стороной 1.
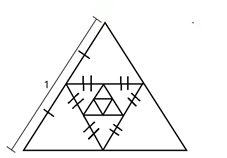
Поделим каждую сторону на две равные части и соединим полученные точки. Получим второй равносторонний треугольник внутри первого со стороной, равной . Вновь поделим пополам каждую из сторон и соединим полученные точки – равносторонний треугольник со стороной , следующий треугольник со стороной , и т.д. Стороны треугольников образуют геометрическую прогрессию со знаменателем заметим, что . Видим, что с ростом n, длины сторон треугольников уменьшаются и приближаются к нулю: при . Такая прогрессия будет бесконечно убывающей.
Геометрическая прогрессия называется бесконечно убывающей, если модуль ее знаменателя меньше 1.
Пример 1
Выяснить, является ли геометрическая прогрессия, заданная формулой n-го члена члена как , бесконечно убывающей.
Решение
Определим, будет ли модуль знаменателя этой прогрессии меньше 1.
.
, значит, по определению, данная последовательность является бесконечно убывающей геометрической прогрессией.
Ответ: является.
Упражнение 1
Выяснить, является ли геометрической прогрессией последовательность, заданная формулой n-го члена члена
Упражнение 2
Выяснить, является ли последовательность, заданная формулой n-го члена как , бесконечно убывающей геометрической прогрессией.
Сумма бесконечно убывающей геометрической прогрессии вычисляется по формуле:
(3)
Эта формула выводится из формулы (2), из той части, где
, значит
Пример 2
Найти сумму бесконечно убывающей геометрической прогрессии, если .
Решение
Найдем , используя формулу (1). Так как , составим систему уравнений
Разделим второе уравнение системы на первое, получим .
Из первого уравнения системы выразим и подставим найденное значение q:
По формуле (3) сумма бесконечно убывающей геометрической прогрессии:
Ответ: 12,8.
Упражнение 3
Найти сумму бесконечно убывающей геометрической прогрессии:
а)
б)
Десятичную периодическую дробь можно представить в виде суммы конечной десятичной дроби и суммы бесконечно убывающей десятичной дроби.
Пример 3
Записать бесконечную периодическую десятичную дробь 2,2(3) в виде обыкновенной.
Решение
2,2(3)=2,2333333333333..
Это число можно записать в следующем виде:
(4)
Члены, начиная со второго, образуют бесконечно убывающую геометрическую прогрессию с .
Найдем сумму этой прогрессии по формуле (3):
.
Тогда сумму (4) можно представить в виде 2,2+.
Ответ: .
Упражнение 4
Записать бесконечную периодическую десятичную дробь в виде обыкновенной:
а) 3,(4); б) 6,03(2); в) 5,28(35).
Пример 4
Вычислить:
а) ;
б) ;
в) .
Решение
а) ;
б) ;
в) .
Ответ: а) -1; б) 25; в) 1.
Итак:
- Геометрическая прогрессия называется бесконечно убывающей, если модуль ее знаменателя меньше единицы.
- Сумма бесконечно убывающей геометрической прогрессии вычисляется по формуле .
Контрольные вопросы
- Дана последовательность, заданная формулой n-го члена. Опишите алгоритм, по которому вы будете определять является ли эта последовательность геометрической прогрессией, бесконечно убывающей геометрической прогрессией.
- Какие вы знаете способы перевода периодической десятичной дроби в обыкновенную дробь. Опишите их.
Упражнение 1
Является.
Упражнение 2
Является.
Упражнение 3
а) ; б) 27.
Упражнение 4
а) ; б) ; в)
- Повторение определения и основных формул геометрической прогрессии
- Введение бесконечно убывающей геометрической прогрессии и ее суммы
- Вычисление суммы бесконечно убывающей геометрической прогрессии
- Запись периодической десятичной дроби в виде обыкновенной с использованием суммы бесконечно убывающей геометрической прогрессии
- Знать, какая прогрессия будет геометрической, бесконечно убывающей геометрической, формулу суммы бесконечно убывающей геометрической прогрессии
- Уметь применять знания на практике
Вспомним определение и основные формулы для геометрической прогрессии.
Геометрическая прогрессия – такая числовая последовательность , что для всех натуральных n выполняется равенство
Формула n-го члена геометрической прогрессии:
(1)
Формула суммы первых n членов геометрической прогрессии:
(2)
- Продолжите фразу «бесконечная непериодическая десятичная дробь называется…». Приведите пример.
- Представьте число в виде периодической дроби.
- Вычислить сумму первых пяти членов геометрической прогрессии, если
Рассмотрим равносторонний треугольник со стороной 1.

Поделим каждую сторону на две равные части и соединим полученные точки. Получим второй равносторонний треугольник внутри первого со стороной, равной . Вновь поделим пополам каждую из сторон и соединим полученные точки – равносторонний треугольник со стороной , следующий треугольник со стороной , и т.д. Стороны треугольников образуют геометрическую прогрессию со знаменателем заметим, что . Видим, что с ростом n, длины сторон треугольников уменьшаются и приближаются к нулю: при . Такая прогрессия будет бесконечно убывающей.
Геометрическая прогрессия называется бесконечно убывающей, если модуль ее знаменателя меньше 1.
Пример 1
Выяснить, является ли геометрическая прогрессия, заданная формулой n-го члена члена как , бесконечно убывающей.
Решение
Определим, будет ли модуль знаменателя этой прогрессии меньше 1.
.
, значит, по определению, данная последовательность является бесконечно убывающей геометрической прогрессией.
Ответ: является.
Упражнение 1
Выяснить, является ли геометрической прогрессией последовательность, заданная формулой n-го члена члена
Упражнение 2
Выяснить, является ли последовательность, заданная формулой n-го члена как , бесконечно убывающей геометрической прогрессией.
Сумма бесконечно убывающей геометрической прогрессии вычисляется по формуле:
(3)
Эта формула выводится из формулы (2), из той части, где
, значит
Пример 2
Найти сумму бесконечно убывающей геометрической прогрессии, если .
Решение
Найдем , используя формулу (1). Так как , составим систему уравнений
Разделим второе уравнение системы на первое, получим .
Из первого уравнения системы выразим и подставим найденное значение q:
По формуле (3) сумма бесконечно убывающей геометрической прогрессии:
Ответ: 12,8.
Упражнение 3
Найти сумму бесконечно убывающей геометрической прогрессии:
а)
б)
Десятичную периодическую дробь можно представить в виде суммы конечной десятичной дроби и суммы бесконечно убывающей десятичной дроби.
Пример 3
Записать бесконечную периодическую десятичную дробь 2,2(3) в виде обыкновенной.
Решение
2,2(3)=2,2333333333333..
Это число можно записать в следующем виде:
(4)
Члены, начиная со второго, образуют бесконечно убывающую геометрическую прогрессию с .
Найдем сумму этой прогрессии по формуле (3):
.
Тогда сумму (4) можно представить в виде 2,2+.
Ответ: .
Упражнение 4
Записать бесконечную периодическую десятичную дробь в виде обыкновенной:
а) 3,(4); б) 6,03(2); в) 5,28(35).
Пример 4
Вычислить:
а) ;
б) ;
в) .
Решение
а) ;
б) ;
в) .
Ответ: а) -1; б) 25; в) 1.
Итак:
- Геометрическая прогрессия называется бесконечно убывающей, если модуль ее знаменателя меньше единицы.
- Сумма бесконечно убывающей геометрической прогрессии вычисляется по формуле .
Контрольные вопросы
- Дана последовательность, заданная формулой n-го члена. Опишите алгоритм, по которому вы будете определять является ли эта последовательность геометрической прогрессией, бесконечно убывающей геометрической прогрессией.
- Какие вы знаете способы перевода периодической десятичной дроби в обыкновенную дробь. Опишите их.
Упражнение 1
Является.
Упражнение 2
Является.
Упражнение 3
а) ; б) 27.
Упражнение 4
а) ; б) ; в)



