- Синус, косинус, тангенс, котангенс
- Основное тригонометрическое тождество. Формулы приведения
- Формулы для вычисления координат точки
- Уметь строить единичную полуокружность.
- Знать, что такое синус и косинус угла из промежутка 0° ≤ ≤ 180º
- Знать понятие тангенс угла , для какого значения тангенс не определён и почему
- Знать понятие котангенс угла , для какого значения котангенс не определён и почему
- Знать и уметь доказывать основное тригонометрическое тождество
- Знать формулы приведения
- Уметь применять формулы приведения при решении задач
- Знать и уметь применять формулы, выражающие координаты точки A с неотрицательной ординатой через длину отрезка OA и угол между лучом OA и положительной полуосью Ox
- Стороны прямоугольного треугольника равны 3 см, 4 см и 5 см. Найдите синус меньшего острого угла этого треугольника
- Стороны прямоугольного треугольника равны 26 м, 24 м и 10 м. Найдите тангенс большего острого угла этого треугольника
- Катет прямоугольного треугольника равен 6 дм, а противолежащий угол равен 30°. Найдите гипотенузу этого треугольника
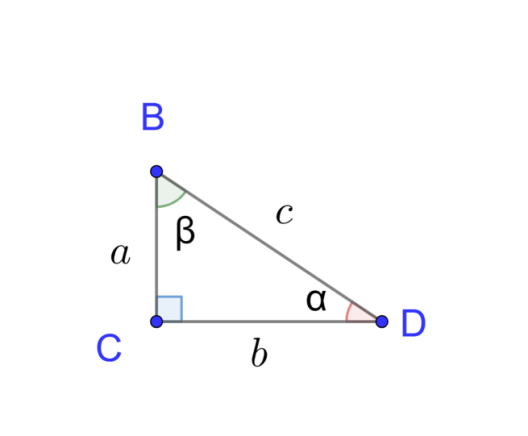 Рис. 1. Прямоугольный треугольник
Рис. 1. Прямоугольный треугольник
Синус, косинус, тангенс, котангенс
В курсе геометрии 8 класса вы познакомились с понятиями синуса, косинуса, тангенса и котангенса для углов прямоугольного треугольника. Вспомним их:
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе: (рис.1).
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе: (рис.1).
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему: (рис.1).
Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему: (рис.1).
Еще мы с вами учили таблицу синусов, косинусов для углов в 30°, 45° и 60°. Вспомним ее:
|
угол,
|
30°
|
45°
|
60°
|
|
sin
|
|
|
|
|
cos
|
|
|
|
|
tg
|
|
1
|
|
|
ctg
|
|
1
|
|
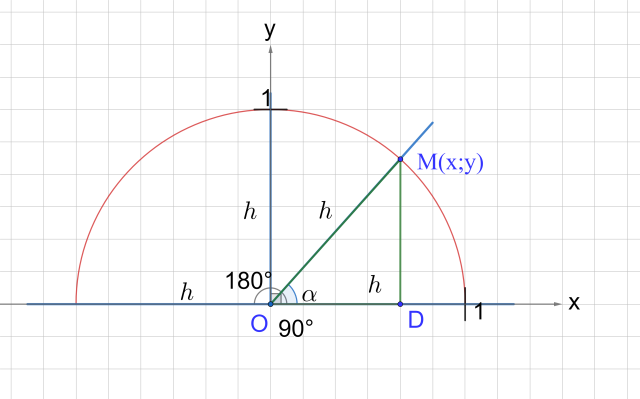 Рис. 2 . Полуокружность
Рис. 2 . Полуокружность
Познакомимся с понятиями синуса, косинуса, тангенса и котангенса произвольного угла из промежутка от 0° до 180º.
Построим в прямоугольной системе координат полуокружность, радиус которой равен 1 так, чтобы центр этой полуокружности совпадал с началом координат (рис. 2).
Такую полуокружность мы назовем единичной полуокружностью. Из точки O проведем произвольный луч h. Этот луч пересекает полуокружность в точке . Угол между лучом h и положительным направлением оси Ox обозначим за . Если луч h совпадает с положительной полуосью абсцисс, то угол равен 0º. Если луч h совпадает с осью Oy, то . Если луч h совпадает с отрицательной полуосью абсцисс, то .
Опустим из точки М перпендикуляр MD на ось Ox и рассмотрим прямоугольный треугольник OMD. Запишем элементы этого треугольника. Поскольку радиус полуокружности равен 1, значит, ОM = 1. Так как координаты точки М равны x и y, то, очевидно, что МD = y, а ОD = x. Тогда . Мы получили, что синус острого угла равен ординате точки М, а косинус острого угла равен абсциссе точки М.
По этим же формулам вычисляются синус и косинус для углов в 90º и 180º.
Для любого угла , 0° ≤ ≤ 180º, синусом угла называется ордината y точки M, а косинусом угла - абсцисса x точки M, где - произвольная точка единичной полуокружности
Поскольку речь у нас идет о единичной полуокружности, то ордината точки может изменяться от 0 до 1, значит, и синус угла из промежутка от 0° до 180º может принимать значения от 0 до 1. Абсцисса точки М может изменяться от -1 до 1, то есть и косинус угла из промежутка от 0° до 180º может изменяться от -1 до 1.
0 ≤ y ≤ 1, следовательно, 0 ≤ ≤ 1;
-1 ≤ x ≤ 1, следовательно, -1 ≤ ≤ 1.
Пример 1
Может ли:
а) абсцисса точки единичной полуокружности быть равной 0,5; ; 5?
б) ордината точки единичной полуокружности быть равной 0,7; 7?
Решение
а) Поскольку полуокружность единичная, значит, абсцисса точки должна принадлежать промежутку от -1 до 1, то есть абсцисса точки может быть равна 0,5; , но не может быть равна 5.
б) Поскольку полуокружность располагается выше оси Ox, то ординаты точек могут быть только из промежутка от 0 до 1, то есть ордината точки может быть равна 0,7; , но не может быть равна ; 7.
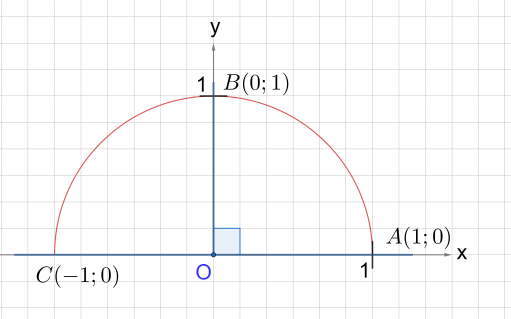 Рис. 3. Полуокружность
Рис. 3. Полуокружность
Для определения sin 0º и cos 0º давайте рассмотрим луч ОА (рис. 3). На единичной полуокружности точка A имеет координаты
(1; 0), значит, sin 0º = y = 0, а cos 0º = x = 1.
Найдем теперь значения sin 90º и
cos 90º. Этот угол задается лучом OB. Координаты точки B равны (0; 1), значит,
sin 90º = y = 1, cos 90º = x = 0.
Проводя аналогичные рассуждения, получим
sin 180º = y = 0, а cos 180º = x = - 1.
Дополним известную нам таблицу синусов косинусов:
|
угол,
|
30°
|
45°
|
60°
|
0°
|
90°
|
180°
|
|
sin
|
|
|
|
0
|
1
|
0
|
|
cos
|
|
|
|
1
|
0
|
1
|
Пример 2
Определить координаты точки M (x; y), лежащей на единичной полуокружности (рис.2), если:
а) = 30°; б) = 45°; в) = 90°.
* - угол между лучом OM и положительной полуосью Ox.
Решение
а) cos 30º = x = sin 30º = y = , следовательно, M ( ).
б) cos 45º = x = sin 45º = y = , следовательно,
M ( ).
в) cos 90º = x = 0; sin 90º = y = 1, следовательно, M (0; 1).
Ответ: а) M( ); б) M( ); в) M(0; 1).
Тангенсом острого угла мы называли отношение синуса этого угла к его косинусу, т.е. . Эта же формула справедлива для произвольного угла от 0º до 180º. Однако, если угол равен 90º, то его косинус равен 0, а значит, мы получим дробь, в знаменателе которой находится 0. Но на 0 делить нельзя, поэтому для угла в 90º тангенс не существует. Таким образом, мы немного уточним определение тангенса.
Тангенсом угла , где 0° ≤ ≤ 180º, ≠ 90º, называется отношение синуса этого угла к его косинусу
Котангенсом острого угла мы называли отношение косинуса этого угла к его синусу, т.е. . Эта же формула справедлива для произвольного угла от 0º до 180º. Однако, если угол равен 0º или 180º, то синус этих углов равен 0, а, значит, мы получим дробь, в знаменателе которой находится 0. Но на 0 делить нельзя, поэтому и не существует. Таким образом, уточним определение котангенса.
Котангенсом угла , где 0° < <180º, называется отношение косинуса этого угла к его синусу
Дополним известную нам таблицу синусов, косинусов, тангенсов и котангенсов:
|
угол,
|
30°
|
45°
|
60°
|
0°
|
90°
|
180°
|
|
sin
|
|
|
|
0
|
1
|
0
|
|
cos
|
|
|
|
1
|
0
|
1
|
|
tg
|
|
1
|
|
0
|
-
|
0
|
|
ctg |
|
1
|
|
-
|
0
|
-
|
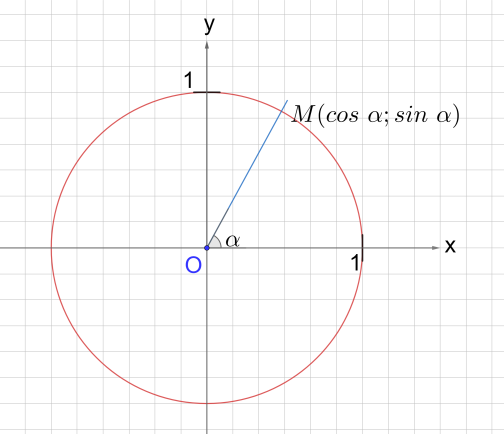 Рис. 4. Окружность (O; 1)
Рис. 4. Окружность (O; 1)
Основное тригонометрическое тождество. Формулы приведения
Вспомним уравнение окружности радиуса r с центром в точке C (x0; y0): .
Уравнение окружности радиуса r с центром в начале координат имеет вид: x2 + y2 = r2.
Наша единичная полуокружность – это часть окружности с центром в начале координат и радиусом, равным 1 (рис.4). Тогда уравнение этой окружности можно записать в виде
x2 + y2 = 1.
То есть координаты всех точек должны удовлетворять этому уравнению.
Но координаты точки окружности есть не что иное, как косинус и синус угла, который соответствует этой точке.
Тогда
Равенство , , называется основным тригонометрическим тождеством.
Пример 3
Найдите sin, если cos =
Решение
;
Ответ: .
 Рис. 5. Полуокружность (O; 1)
Рис. 5. Полуокружность (O; 1)
Вернемся к единичной полуокружности и проведем два луча ОМ и OB (рис. 5).
Из точки М опустим два перпендикуляра к осям Oy и Ox и обозначим точки пересечения этих прямых с осями точками C и D соответственно.
Очевидно, ∠DOB = 90°. Если ∠DOM = то ∠BOM = 90° - . Рассмотрим DОМ и
МОC. Это прямоугольные треугольники с общей гипотенузой ОМ: , CM = OD, следовательно, , OC = DM, следовательно,
Посмотрим на полученные равенства.
Итак, если 0° ≤ ≤ 90º, то
Аналогично выводятся формулы , для всех углов из промежутка от 0º до 180º. Эти формулы называются формулами приведения.
Итак,
Если 0° ≤ ≤ 90º, то
.
Если 0° ≤ ≤ 180º, то
.
Проверим выполнение этих формул на конкретном примере.
Пример 4
Вычислите а) sin 30º; б) sin 120º.
Решение
а)
б)
Ответ: a); б)
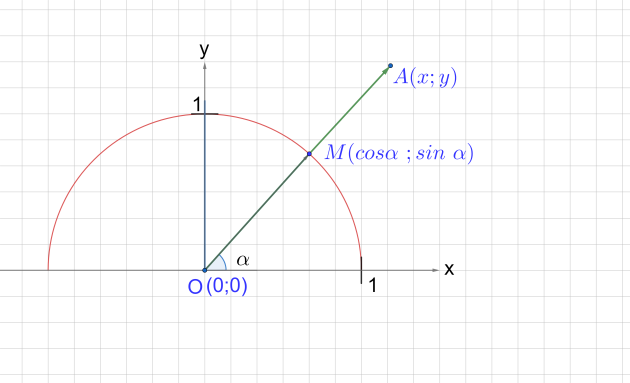 Рис. 6. Полуокружность (O; 1)
Рис. 6. Полуокружность (O; 1)
Формулы для вычисления координат точки
Рассмотрим задачу: необходимо определить координаты точки A, которая расположена в верхней координатной полуплоскости. Построим в этой полуплоскости единичную полуокружность. Соединим точку A с центром полуокружности, обозначим за М точку пересечения отрезка ОА и полуокружности.
Координаты точки M равны и соответственно (рис. 6). Вектор имеет те же координаты (как радиус-вектор точки), что и точка M, т. е. .
, , тогда , . Но, с другой стороны, у вектора координаты и соответственно. Тогда , , т. е. .
Проанализируем знаки координат точки A. Координаты точки зависят от величины отрезка ОА, (а это всегда положительное число), и от знака синуса и косинуса угла . Синус произвольного угла из промежутка от 0°до 180º находится в промежутке от 0 до 1, то есть принимает неотрицательные значения. Косинус угла может принимать значения от -1 до 1, то есть быть как положительным, так и отрицательным. Значит, можно записать, что y ≥ 0 при
0° ≤ ≤ 180º; x ≥ 0 при 0° ≤ ≤ 90º и x < 0 при 90° < ≤ 180º.
Пример 5
Угол между лучом OA, пересекающим единичную полуокружность, и положительной полуосью Ox равен . Найдите координаты точки
A (x; y), если OA = 3 и =45º.
Решение
1.
2. значит,
3. , значит,
4. A (; ).
Ответ: A (; ).
Упражнение 1
1. Может ли: а) абсцисса точки единичной полуокружности быть равной 0,6; ; ; 4?
б) ордината точки единичной полуокружности быть равна 0,5; ; ; 6?
2. Определите координаты точки M (x; y), лежащей на единичной полуокружности (рис.2), если:
а) = 60°; б) = 180°.
* - угол между лучом OM и положительной полуосью Ox
3. Вычислите а) cos 30º; б) cos 120º.
4. Угол между лучом OA, пересекающим единичную полуокружность, и положительной полуосью Ox равен . Найдите координаты точки
A (x; y), если OA = 2 и = 30º.
Контрольные вопросы
1. Начертите оси координат и постройте единичную полуокружность.
2. Объясните, что такое синус и косинус угла из промежутка
0° ≤ ≤ 180º.
3. Что называется тангенсом угла ? Для какого значения тангенс не определён и почему?
4. Что называется котангенсом угла ? Для какого значения котангенс не определён и почему?
5. Докажите основное тригонометрическое тождество.
6. Напишите формулы приведения.
7. Назовите формулы, выражающие координаты точки A с неотрицательной ординатой через длину отрезка OA и угол между лучом OA и положительной полуосью Ox.
Ответы
- а) 0,6; ; - может; 4 – не может; б) 0,5; – может; ; 6 – не может.
- а) M (; ); б) M (-1; 0).
- а) ; б) .
- A(; 1).
- Синус, косинус, тангенс, котангенс
- Основное тригонометрическое тождество. Формулы приведения
- Формулы для вычисления координат точки
- Уметь строить единичную полуокружность.
- Знать, что такое синус и косинус угла из промежутка 0° ≤ ≤ 180º
- Знать понятие тангенс угла , для какого значения тангенс не определён и почему
- Знать понятие котангенс угла , для какого значения котангенс не определён и почему
- Знать и уметь доказывать основное тригонометрическое тождество
- Знать формулы приведения
- Уметь применять формулы приведения при решении задач
- Знать и уметь применять формулы, выражающие координаты точки A с неотрицательной ординатой через длину отрезка OA и угол между лучом OA и положительной полуосью Ox
- Стороны прямоугольного треугольника равны 3 см, 4 см и 5 см. Найдите синус меньшего острого угла этого треугольника
- Стороны прямоугольного треугольника равны 26 м, 24 м и 10 м. Найдите тангенс большего острого угла этого треугольника
- Катет прямоугольного треугольника равен 6 дм, а противолежащий угол равен 30°. Найдите гипотенузу этого треугольника
 Рис. 1. Прямоугольный треугольник
Рис. 1. Прямоугольный треугольник
Синус, косинус, тангенс, котангенс
В курсе геометрии 8 класса вы познакомились с понятиями синуса, косинуса, тангенса и котангенса для углов прямоугольного треугольника. Вспомним их:
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе: (рис.1).
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе: (рис.1).
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему: (рис.1).
Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему: (рис.1).
Еще мы с вами учили таблицу синусов, косинусов для углов в 30°, 45° и 60°. Вспомним ее:
|
угол,
|
30°
|
45°
|
60°
|
|
sin
|
|
|
|
|
cos
|
|
|
|
|
tg
|
|
1
|
|
|
ctg
|
|
1
|
|
 Рис. 2 . Полуокружность
Рис. 2 . Полуокружность
Познакомимся с понятиями синуса, косинуса, тангенса и котангенса произвольного угла из промежутка от 0° до 180º.
Построим в прямоугольной системе координат полуокружность, радиус которой равен 1 так, чтобы центр этой полуокружности совпадал с началом координат (рис. 2).
Такую полуокружность мы назовем единичной полуокружностью. Из точки O проведем произвольный луч h. Этот луч пересекает полуокружность в точке . Угол между лучом h и положительным направлением оси Ox обозначим за . Если луч h совпадает с положительной полуосью абсцисс, то угол равен 0º. Если луч h совпадает с осью Oy, то . Если луч h совпадает с отрицательной полуосью абсцисс, то .
Опустим из точки М перпендикуляр MD на ось Ox и рассмотрим прямоугольный треугольник OMD. Запишем элементы этого треугольника. Поскольку радиус полуокружности равен 1, значит, ОM = 1. Так как координаты точки М равны x и y, то, очевидно, что МD = y, а ОD = x. Тогда . Мы получили, что синус острого угла равен ординате точки М, а косинус острого угла равен абсциссе точки М.
По этим же формулам вычисляются синус и косинус для углов в 90º и 180º.
Для любого угла , 0° ≤ ≤ 180º, синусом угла называется ордината y точки M, а косинусом угла - абсцисса x точки M, где - произвольная точка единичной полуокружности
Поскольку речь у нас идет о единичной полуокружности, то ордината точки может изменяться от 0 до 1, значит, и синус угла из промежутка от 0° до 180º может принимать значения от 0 до 1. Абсцисса точки М может изменяться от -1 до 1, то есть и косинус угла из промежутка от 0° до 180º может изменяться от -1 до 1.
0 ≤ y ≤ 1, следовательно, 0 ≤ ≤ 1;
-1 ≤ x ≤ 1, следовательно, -1 ≤ ≤ 1.
Пример 1
Может ли:
а) абсцисса точки единичной полуокружности быть равной 0,5; ; 5?
б) ордината точки единичной полуокружности быть равной 0,7; 7?
Решение
а) Поскольку полуокружность единичная, значит, абсцисса точки должна принадлежать промежутку от -1 до 1, то есть абсцисса точки может быть равна 0,5; , но не может быть равна 5.
б) Поскольку полуокружность располагается выше оси Ox, то ординаты точек могут быть только из промежутка от 0 до 1, то есть ордината точки может быть равна 0,7; , но не может быть равна ; 7.
 Рис. 3. Полуокружность
Рис. 3. Полуокружность
Для определения sin 0º и cos 0º давайте рассмотрим луч ОА (рис. 3). На единичной полуокружности точка A имеет координаты
(1; 0), значит, sin 0º = y = 0, а cos 0º = x = 1.
Найдем теперь значения sin 90º и
cos 90º. Этот угол задается лучом OB. Координаты точки B равны (0; 1), значит,
sin 90º = y = 1, cos 90º = x = 0.
Проводя аналогичные рассуждения, получим
sin 180º = y = 0, а cos 180º = x = - 1.
Дополним известную нам таблицу синусов косинусов:
|
угол,
|
30°
|
45°
|
60°
|
0°
|
90°
|
180°
|
|
sin
|
|
|
|
0
|
1
|
0
|
|
cos
|
|
|
|
1
|
0
|
1
|
Пример 2
Определить координаты точки M (x; y), лежащей на единичной полуокружности (рис.2), если:
а) = 30°; б) = 45°; в) = 90°.
* - угол между лучом OM и положительной полуосью Ox.
Решение
а) cos 30º = x = sin 30º = y = , следовательно, M ( ).
б) cos 45º = x = sin 45º = y = , следовательно,
M ( ).
в) cos 90º = x = 0; sin 90º = y = 1, следовательно, M (0; 1).
Ответ: а) M( ); б) M( ); в) M(0; 1).
Тангенсом острого угла мы называли отношение синуса этого угла к его косинусу, т.е. . Эта же формула справедлива для произвольного угла от 0º до 180º. Однако, если угол равен 90º, то его косинус равен 0, а значит, мы получим дробь, в знаменателе которой находится 0. Но на 0 делить нельзя, поэтому для угла в 90º тангенс не существует. Таким образом, мы немного уточним определение тангенса.
Тангенсом угла , где 0° ≤ ≤ 180º, ≠ 90º, называется отношение синуса этого угла к его косинусу
Котангенсом острого угла мы называли отношение косинуса этого угла к его синусу, т.е. . Эта же формула справедлива для произвольного угла от 0º до 180º. Однако, если угол равен 0º или 180º, то синус этих углов равен 0, а, значит, мы получим дробь, в знаменателе которой находится 0. Но на 0 делить нельзя, поэтому и не существует. Таким образом, уточним определение котангенса.
Котангенсом угла , где 0° < <180º, называется отношение косинуса этого угла к его синусу
Дополним известную нам таблицу синусов, косинусов, тангенсов и котангенсов:
|
угол,
|
30°
|
45°
|
60°
|
0°
|
90°
|
180°
|
|
sin
|
|
|
|
0
|
1
|
0
|
|
cos
|
|
|
|
1
|
0
|
1
|
|
tg
|
|
1
|
|
0
|
-
|
0
|
|
ctg |
|
1
|
|
-
|
0
|
-
|
 Рис. 4. Окружность (O; 1)
Рис. 4. Окружность (O; 1)
Основное тригонометрическое тождество. Формулы приведения
Вспомним уравнение окружности радиуса r с центром в точке C (x0; y0): .
Уравнение окружности радиуса r с центром в начале координат имеет вид: x2 + y2 = r2.
Наша единичная полуокружность – это часть окружности с центром в начале координат и радиусом, равным 1 (рис.4). Тогда уравнение этой окружности можно записать в виде
x2 + y2 = 1.
То есть координаты всех точек должны удовлетворять этому уравнению.
Но координаты точки окружности есть не что иное, как косинус и синус угла, который соответствует этой точке.
Тогда
Равенство , , называется основным тригонометрическим тождеством.
Пример 3
Найдите sin, если cos =
Решение
;
Ответ: .
 Рис. 5. Полуокружность (O; 1)
Рис. 5. Полуокружность (O; 1)
Вернемся к единичной полуокружности и проведем два луча ОМ и OB (рис. 5).
Из точки М опустим два перпендикуляра к осям Oy и Ox и обозначим точки пересечения этих прямых с осями точками C и D соответственно.
Очевидно, ∠DOB = 90°. Если ∠DOM = то ∠BOM = 90° - . Рассмотрим DОМ и
МОC. Это прямоугольные треугольники с общей гипотенузой ОМ: , CM = OD, следовательно, , OC = DM, следовательно,
Посмотрим на полученные равенства.
Итак, если 0° ≤ ≤ 90º, то
Аналогично выводятся формулы , для всех углов из промежутка от 0º до 180º. Эти формулы называются формулами приведения.
Итак,
Если 0° ≤ ≤ 90º, то
.
Если 0° ≤ ≤ 180º, то
.
Проверим выполнение этих формул на конкретном примере.
Пример 4
Вычислите а) sin 30º; б) sin 120º.
Решение
а)
б)
Ответ: a); б)
 Рис. 6. Полуокружность (O; 1)
Рис. 6. Полуокружность (O; 1)
Формулы для вычисления координат точки
Рассмотрим задачу: необходимо определить координаты точки A, которая расположена в верхней координатной полуплоскости. Построим в этой полуплоскости единичную полуокружность. Соединим точку A с центром полуокружности, обозначим за М точку пересечения отрезка ОА и полуокружности.
Координаты точки M равны и соответственно (рис. 6). Вектор имеет те же координаты (как радиус-вектор точки), что и точка M, т. е. .
, , тогда , . Но, с другой стороны, у вектора координаты и соответственно. Тогда , , т. е. .
Проанализируем знаки координат точки A. Координаты точки зависят от величины отрезка ОА, (а это всегда положительное число), и от знака синуса и косинуса угла . Синус произвольного угла из промежутка от 0°до 180º находится в промежутке от 0 до 1, то есть принимает неотрицательные значения. Косинус угла может принимать значения от -1 до 1, то есть быть как положительным, так и отрицательным. Значит, можно записать, что y ≥ 0 при
0° ≤ ≤ 180º; x ≥ 0 при 0° ≤ ≤ 90º и x < 0 при 90° < ≤ 180º.
Пример 5
Угол между лучом OA, пересекающим единичную полуокружность, и положительной полуосью Ox равен . Найдите координаты точки
A (x; y), если OA = 3 и =45º.
Решение
1.
2. значит,
3. , значит,
4. A (; ).
Ответ: A (; ).
Упражнение 1
1. Может ли: а) абсцисса точки единичной полуокружности быть равной 0,6; ; ; 4?
б) ордината точки единичной полуокружности быть равна 0,5; ; ; 6?
2. Определите координаты точки M (x; y), лежащей на единичной полуокружности (рис.2), если:
а) = 60°; б) = 180°.
* - угол между лучом OM и положительной полуосью Ox
3. Вычислите а) cos 30º; б) cos 120º.
4. Угол между лучом OA, пересекающим единичную полуокружность, и положительной полуосью Ox равен . Найдите координаты точки
A (x; y), если OA = 2 и = 30º.
Контрольные вопросы
1. Начертите оси координат и постройте единичную полуокружность.
2. Объясните, что такое синус и косинус угла из промежутка
0° ≤ ≤ 180º.
3. Что называется тангенсом угла ? Для какого значения тангенс не определён и почему?
4. Что называется котангенсом угла ? Для какого значения котангенс не определён и почему?
5. Докажите основное тригонометрическое тождество.
6. Напишите формулы приведения.
7. Назовите формулы, выражающие координаты точки A с неотрицательной ординатой через длину отрезка OA и угол между лучом OA и положительной полуосью Ox.
Ответы
- а) 0,6; ; - может; 4 – не может; б) 0,5; – может; ; 6 – не может.
- а) M (; ); б) M (-1; 0).
- а) ; б) .
- A(; 1).



