- Смешанное соединение проводников. Метод эквивалентных преобразований
- Примеры решения задач
- знать понятие «смешанное соединение проводников»; метод эквивалентных преобразований
- уметь рассчитывать электрические схемы со смешанным соединением проводников
- Как найти общее напряжение при последовательном соединении проводников?
- Как найти общее сопротивление при последовательном соединении проводников?
- Как найти общее сопротивление при параллельном соединении проводников?
Смешанное соединение проводников. Метод эквивалентных преобразований
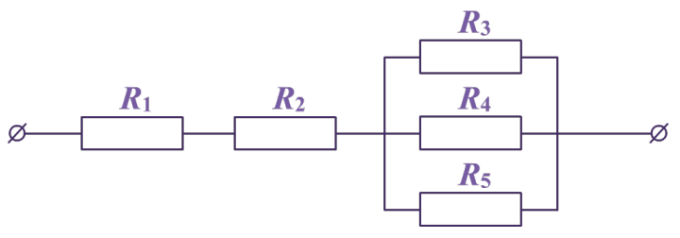 Рис. 1. Смешанное соединение проводников
Рис. 1. Смешанное соединение проводников
Рассмотрим схему, представленную на рисунке 1.
Резисторы с сопротивлениями R1 и R2 соединены между собой последовательно, резисторы R3, R4 и R5 — параллельно.
Если в электрической цепи одновременно присутствуют и последовательное, и параллельное соединения проводников, такое соединение называют смешанным.
Для расчёта электрической цепи, содержащей смешанное соединение, используют метод эквивалентных преобразований. Суть данного метода заключается в том, что исходную электрическую цепь заменяют на более простую электрическую цепь, при этом распределение сил токов и напряжений в непреобразованной части цепи остаётся прежним.
Например, в изображённой на рисунке 1 схеме проводники с сопротивлениями R3, R4 и R5 можно заменить на один проводник, сопротивление которого R345 равно общему сопротивлению трёх данных резисторов:
.
 Рис. 2. Эквивалентная схема
Рис. 2. Эквивалентная схема
Тогда исходную электрическую цепь можно заменить на эквивалентную схему, состоящую из трёх последовательно соединённых проводников с сопротивлениями R1, R2 и R345 (рис. 2).
При этом распределение сил токов и напряжений на резисторах R1 и R2 останется таким же, каким было до преобразования электрической цепи.
Примеры решения задач
Пример 1
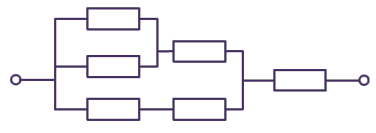 Рис. 3. Иллюстрация к примеру 1
Рис. 3. Иллюстрация к примеру 1
Найти общее сопротивление участка цепи, представленного на рисунке 3, если сопротивления всех резисторов одинаковы и равны R = 2 Ом.
Решение
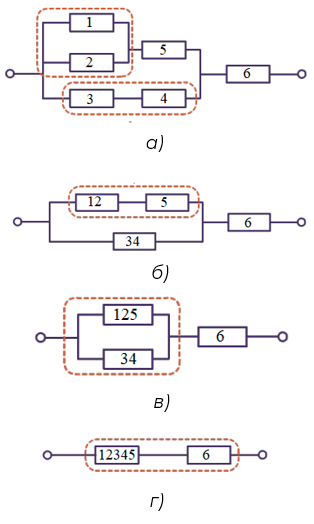 Рис. 4. Эквивалентные схемы сложной цепи
Рис. 4. Эквивалентные схемы сложной цепи
Пронумеруем резисторы (рис. 4, а). Проводники 1 и 2 соединены параллельно, найдём их общее сопротивление R12:
;
.
Проводники 3 и 4 соединены последовательно, найдём их общее сопротивление R34:
.
Проводники 1 и 2 можно заменить на один проводник сопротивлением R12, проводники 3 и 4 — на проводник R34. В результате получаем упрощённую эквивалентную схему, представленную на рисунке 4, б.
Из рисунка 4, б видно, что проводники 12 и 5 соединены последовательно, найдём их общее сопротивление R125:
.
Заменяем два проводника 12 и 5 на один проводник сопротивлением R125, получаем эквивалентную схему, состоящую из трёх резисторов
(рис. 4, в). Находим общее сопротивление проводников 125 и 34:
;
.
В результате преобразований получаем схему, состоящую из двух последовательно соединённых проводников с сопротивлениями R12345 и R6 (рис. 4, г).
.
Ответ: .
Пример 2
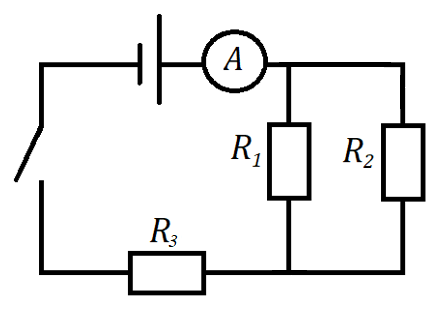 Рис. 5. Иллюстрация к примеру 2
Рис. 5. Иллюстрация к примеру 2
Рассчитайте электрическую цепь, изображённую на рисунке 5. Амперметр показывает силу тока 2 А. Сопротивления первого, второго и третьего резисторов равны 4, 6 и 0,6 Ом соответственно.
Решение
Прежде всего, рассчитаем общее сопротивление цепи. Резисторы 1 и 2 соединены параллельно, найдём их общее сопротивление:
;
.
Исходной схеме эквивалента схема из двух проводников сопротивлениями R12 и R3, соединённых последовательно. Тогда общее сопротивление данной цепи равно:
.
Амперметр находится в неразветвлённой части цепи, следовательно, он показывает общую силу тока в цепи, одинаковую на проводниках, соединённых последовательно:
.
Найдём общее напряжение, а также напряжение на проводниках 12 и 3, используя закон Ома:
;
;
.
Осталось найти распределение сил токов и напряжений на проводниках 1 и 2. Данные резисторы соединены параллельно, следовательно, напряжения на данных резисторах одинаковы и равны общему напряжению на данном участке цепи:
.
Сопротивления резисторов 1 и 2 известны, находим силы токов на данных проводниках по закону Ома:
;
.
Ответ: ; ; ; ; ; ; .
Пример 3
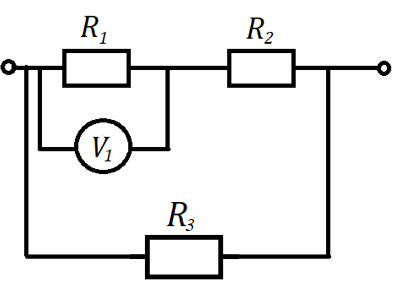 Рис. 6. Иллюстрация к примеру 3
Рис. 6. Иллюстрация к примеру 3
Найти общую силу тока в электрической цепи, изображённой на рисунке 6. Вольтметр показывает напряжение 21 В. Сопротивления первого, второго и третьего резисторов равны 3, 2 и 5 Ом соответственно.
Решение
Из условия задачи известны сопротивление и напряжение на первом резисторе, найдём силу тока на данном проводнике:
.
Так как проводники 1 и 2 соединены последовательно, сила тока на них одинакова:
.
Используя закон Ома, найдём напряжение на втором резисторе:
.
Так как проводники 1 и 2 соединены последовательно, общее напряжение на данном участке равно сумме напряжений на данных резисторах:
.
Участок цепи, изображённый на рисунке 6, можно представить в виде упрощённой схемы, состоящей из двух параллельно соединённых проводников с сопротивлениями R12 и R3. Тогда напряжение на данных резисторах одинаково и равно общему напряжению на данном участке:
.
Найдём силу тока на третьем резисторе:
.
Общая сила тока равна сумме сил тока на проводниках 12 и 3:
.
Ответ: .
Упражнение 1
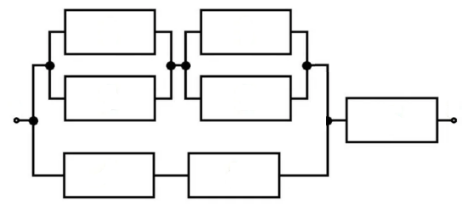 Рис. 7
Рис. 7
1. Рассчитайте общее сопротивление участка цепи, представленного на рисунке 7, если сопротивления всех резисторов одинаковы и равны R = 2 Ом.
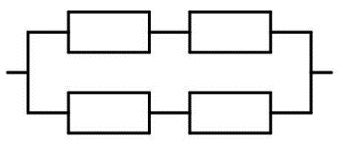 Рис. 8
Рис. 8
2. Рассчитайте электрическую цепь, представленную на рисунке 8, если сопротивления всех резисторов одинаковы и равны 4 Ом. Сила тока в неразветвлённой части цепи равна 50 А.
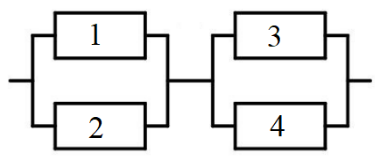 Рис. 9
Рис. 9
3. Сопротивления резисторов 1, 2, 3 и 4 равны 2, 3, 7 и 3 Ом соответственно
(рис. 9). Известно, что напряжение на резисторе 1 составляет 20 В. Найти распределение сил токов и напряжений на данном участке цепи.
Упражнение 1
1. R = 3,3 Ом
2. I1 = I2 = I3 = I4 = 25 А; U = 200 В; U1 = U2 = U3 = U4 = 100 В
3. I = 16,7 А; I1 = 10 А; I2 = 6,7 А; I3 = 5 А; I4 = 11,7 А; U = 55,07 В;
U2 = 20 В; U3 = U4 = 35,07 В
- Смешанное соединение проводников. Метод эквивалентных преобразований
- Примеры решения задач
- знать понятие «смешанное соединение проводников»; метод эквивалентных преобразований
- уметь рассчитывать электрические схемы со смешанным соединением проводников
- Как найти общее напряжение при последовательном соединении проводников?
- Как найти общее сопротивление при последовательном соединении проводников?
- Как найти общее сопротивление при параллельном соединении проводников?
Смешанное соединение проводников. Метод эквивалентных преобразований
 Рис. 1. Смешанное соединение проводников
Рис. 1. Смешанное соединение проводников
Рассмотрим схему, представленную на рисунке 1.
Резисторы с сопротивлениями R1 и R2 соединены между собой последовательно, резисторы R3, R4 и R5 — параллельно.
Если в электрической цепи одновременно присутствуют и последовательное, и параллельное соединения проводников, такое соединение называют смешанным.
Для расчёта электрической цепи, содержащей смешанное соединение, используют метод эквивалентных преобразований. Суть данного метода заключается в том, что исходную электрическую цепь заменяют на более простую электрическую цепь, при этом распределение сил токов и напряжений в непреобразованной части цепи остаётся прежним.
Например, в изображённой на рисунке 1 схеме проводники с сопротивлениями R3, R4 и R5 можно заменить на один проводник, сопротивление которого R345 равно общему сопротивлению трёх данных резисторов:
.
 Рис. 2. Эквивалентная схема
Рис. 2. Эквивалентная схема
Тогда исходную электрическую цепь можно заменить на эквивалентную схему, состоящую из трёх последовательно соединённых проводников с сопротивлениями R1, R2 и R345 (рис. 2).
При этом распределение сил токов и напряжений на резисторах R1 и R2 останется таким же, каким было до преобразования электрической цепи.
Примеры решения задач
Пример 1
 Рис. 3. Иллюстрация к примеру 1
Рис. 3. Иллюстрация к примеру 1
Найти общее сопротивление участка цепи, представленного на рисунке 3, если сопротивления всех резисторов одинаковы и равны R = 2 Ом.
Решение
 Рис. 4. Эквивалентные схемы сложной цепи
Рис. 4. Эквивалентные схемы сложной цепи
Пронумеруем резисторы (рис. 4, а). Проводники 1 и 2 соединены параллельно, найдём их общее сопротивление R12:
;
.
Проводники 3 и 4 соединены последовательно, найдём их общее сопротивление R34:
.
Проводники 1 и 2 можно заменить на один проводник сопротивлением R12, проводники 3 и 4 — на проводник R34. В результате получаем упрощённую эквивалентную схему, представленную на рисунке 4, б.
Из рисунка 4, б видно, что проводники 12 и 5 соединены последовательно, найдём их общее сопротивление R125:
.
Заменяем два проводника 12 и 5 на один проводник сопротивлением R125, получаем эквивалентную схему, состоящую из трёх резисторов
(рис. 4, в). Находим общее сопротивление проводников 125 и 34:
;
.
В результате преобразований получаем схему, состоящую из двух последовательно соединённых проводников с сопротивлениями R12345 и R6 (рис. 4, г).
.
Ответ: .
Пример 2
 Рис. 5. Иллюстрация к примеру 2
Рис. 5. Иллюстрация к примеру 2
Рассчитайте электрическую цепь, изображённую на рисунке 5. Амперметр показывает силу тока 2 А. Сопротивления первого, второго и третьего резисторов равны 4, 6 и 0,6 Ом соответственно.
Решение
Прежде всего, рассчитаем общее сопротивление цепи. Резисторы 1 и 2 соединены параллельно, найдём их общее сопротивление:
;
.
Исходной схеме эквивалента схема из двух проводников сопротивлениями R12 и R3, соединённых последовательно. Тогда общее сопротивление данной цепи равно:
.
Амперметр находится в неразветвлённой части цепи, следовательно, он показывает общую силу тока в цепи, одинаковую на проводниках, соединённых последовательно:
.
Найдём общее напряжение, а также напряжение на проводниках 12 и 3, используя закон Ома:
;
;
.
Осталось найти распределение сил токов и напряжений на проводниках 1 и 2. Данные резисторы соединены параллельно, следовательно, напряжения на данных резисторах одинаковы и равны общему напряжению на данном участке цепи:
.
Сопротивления резисторов 1 и 2 известны, находим силы токов на данных проводниках по закону Ома:
;
.
Ответ: ; ; ; ; ; ; .
Пример 3
 Рис. 6. Иллюстрация к примеру 3
Рис. 6. Иллюстрация к примеру 3
Найти общую силу тока в электрической цепи, изображённой на рисунке 6. Вольтметр показывает напряжение 21 В. Сопротивления первого, второго и третьего резисторов равны 3, 2 и 5 Ом соответственно.
Решение
Из условия задачи известны сопротивление и напряжение на первом резисторе, найдём силу тока на данном проводнике:
.
Так как проводники 1 и 2 соединены последовательно, сила тока на них одинакова:
.
Используя закон Ома, найдём напряжение на втором резисторе:
.
Так как проводники 1 и 2 соединены последовательно, общее напряжение на данном участке равно сумме напряжений на данных резисторах:
.
Участок цепи, изображённый на рисунке 6, можно представить в виде упрощённой схемы, состоящей из двух параллельно соединённых проводников с сопротивлениями R12 и R3. Тогда напряжение на данных резисторах одинаково и равно общему напряжению на данном участке:
.
Найдём силу тока на третьем резисторе:
.
Общая сила тока равна сумме сил тока на проводниках 12 и 3:
.
Ответ: .
Упражнение 1
 Рис. 7
Рис. 7
1. Рассчитайте общее сопротивление участка цепи, представленного на рисунке 7, если сопротивления всех резисторов одинаковы и равны R = 2 Ом.
 Рис. 8
Рис. 8
2. Рассчитайте электрическую цепь, представленную на рисунке 8, если сопротивления всех резисторов одинаковы и равны 4 Ом. Сила тока в неразветвлённой части цепи равна 50 А.
 Рис. 9
Рис. 9
3. Сопротивления резисторов 1, 2, 3 и 4 равны 2, 3, 7 и 3 Ом соответственно
(рис. 9). Известно, что напряжение на резисторе 1 составляет 20 В. Найти распределение сил токов и напряжений на данном участке цепи.
Упражнение 1
1. R = 3,3 Ом
2. I1 = I2 = I3 = I4 = 25 А; U = 200 В; U1 = U2 = U3 = U4 = 100 В
3. I = 16,7 А; I1 = 10 А; I2 = 6,7 А; I3 = 5 А; I4 = 11,7 А; U = 55,07 В;
U2 = 20 В; U3 = U4 = 35,07 В



