- Конденсаторы
- Электрическая ёмкость конденсатора
- Электроёмкость плоского конденсатора
- Энергия заряжённого конденсатора
- знать, что такое конденсатор
- знать, как определяется электрическая ёмкость конденсатора
- уметь рассчитывать электроёмкость плоского конденсатора
- уметь находить энергию заряжённого конденсатора различными способами
- Какие тела называют проводниками?
- Что такое диэлектрическая проницаемость вещества?
- Выполняется ли принцип суперпозиции для электрических сил?
Конденсаторы
Из курса физики 8 класса вам известно, что ток — это упорядоченное движение заряжённых частиц. Описанные ранее способы разделения разноимённо электрических зарядов — электризация при соприкосновении, электростатическая индукция — позволяют получить на поверхности тел лишь сравнительно небольшое число свободных электрических зарядов. В случае если потребуется накопление солидного количества разноимённых электрических зарядов, то применяется такой прибор, как конденсатор. Конденсаторы применяются в электронных, радиотехнических и электрических устройствах. Если вы разберете любой электроприбор, работающий не от сети, то обязательно встретите его там.
Конденсатор — система, состоящая из двух проводников (обкладок), разделённых слоем диэлектрика, толщина которого мала по сравнению с размерами проводников.
Плоский конденсатор — система, которая состоит из двух плоских параллельных пластин, заряжённых равными по модулю зарядами противоположного знака и разделённых слоем диэлектрика.
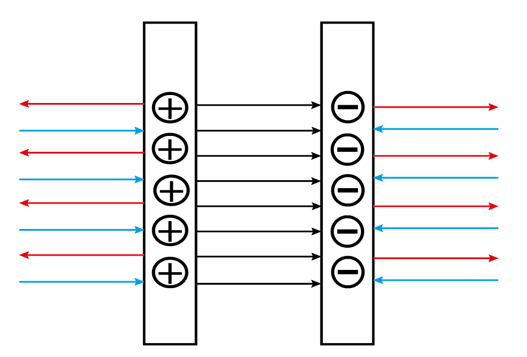 Рис. 1. Напряжённость плоского конденсатора
Рис. 1. Напряжённость плоского конденсатора
При зарядке обкладкам конденсатора сообщают равные по модулю разноимённые заряды. Если пластинам плоского конденсатора сообщить равные по модулю заряды, но противоположные по знаку, то напряжённость электрического поля между пластинами будет в два раза больше, чем напряжённость электрического поля у одной пластины. Вне пластин напряжённость электрического поля равна нулю, так как равные заряды разного знака на двух пластинах создают вне пластин электрические поля, напряжённости которых равны по модулю, но противоположны по направлению (рис. 1). Отметим, что именно заряд положительно заряжённой пластины называют зарядом конденсатора.
Электрическая ёмкость конденсатора
Эксперименты показывают, что напряжение между пластинами конденсатора прямо пропорционально его заряду . Это позволяет ввести физическую величину, характеризующую способность конденсатора накапливать электрический заряд.
Отношение заряда конденсатора к модулю напряжения между его пластинами называют электрической ёмкостью конденсатора:
.
При неизменном расположении пластин электроёмкость конденсатора является постоянной величиной при любом заряде на пластинах.
Единица измерения ёмкости в СИ — фарад (Ф). Электроёмкостью в 1 Ф обладает такой конденсатор, напряжение которого равно 1 В при сообщении обкладкам разноимённых зарядов по 1 Кл.
Отметим, что 1 Ф — очень большая ёмкость, поэтому на практике широко используются дольные единицы электроёмкости — микрофарад (мкФ), нанофарад (нФ) и пикофарад (пФ):
1 мкФ = 10−6 Ф;
1 нФ = 10−9 Ф;
1 пФ = 10−12 Ф.
Электроёмкость плоского конденсатора
Напряжённость поля между двумя пластинами плоского конденсатора равна сумме напряжённостей полей, создаваемых каждой из пластин:
.
Если на пластинах площадью находятся электрические заряды и , то на основании известной формулы для напряжённости электрического поля бесконечной плоскости с поверхностной плотностью зарядов
 Рис. 2. Плоский конденсатор
Рис. 2. Плоский конденсатор
можно записать для модуля напряжённости поля между пластинами следующее выражение:
.
Для однородного электрического поля связь между напряжённостью и напряжением даётся выражением
,
где — в данном случае расстояние между пластинами, — напряжение на конденсаторе.
Подставим вышеизложенные формулы в выражение для электроёмкости конденсатора:
.
.
Энергия заряжённого конденсатора
Зарядим конденсатор и затем подключим к его выводам электрическую лампочку. При подключении лампочки в цепь наблюдается кратковременная вспышка света. Из этого опыта следует, что заряжённый конденсатор обладает энергией.
Если на обкладках конденсатора электроёмкостью находятся электрические разноимённые заряды и , то согласно выражению для электроёмкости напряжение между обкладками конденсатора можно выразить как
.
В процессе разрядки конденсатора напряжение между его обкладками убывает прямо пропорционально заряду от первоначального напряжения до 0. Среднее значение напряжения в процессе разрядки равно
.
Работа по переносу заряда между двумя точками в электростатическом поле пропорциональна разности потенциалов в этих двух точках. Тогда для работы , совершаемой электрическим полем при разрядке конденсатора, будем иметь следующий вид:
.
Таким образом, энергия электрического поля заряжённого конденсатора может найдена по следующим формулам
.
Наличие диэлектрика между пластинами конденсатора не изменит формулу для энергии электрического поля. Внесение диэлектрика между пластинами уменьшит напряжённость поля в раз. Тогда с учётом диэлектрика можно записать
.
Видно, что результат остаётся тем же. Также полученные формулы для расчёта энергии электрического поля заряжённого конденсатора справедливы не только для плоских конденсаторов, но и для конденсаторов любой формы.
Пример 1
Определите заряд и энергию электрического поля конденсатора ёмкостью = 5 нФ, если напряжение между его обкладками = 80 В.
Решение
1. Взаимосвязь между зарядом, ёмкостью и напряжением задаётся следующей формулой:
.
Отсюда найдём заряд:
.
2. Найдём энергию электрического поля конденсатора:
.
Ответ: , .
Упражнение 1
1. Напряжение между пластинами плоского воздушного конденсатора
= 239 В, а расстояние между ними = 1 мм. Определите напряжённость электрического поля между пластинами конденсатора.
2. Площадь каждой пластины плоского конденсатора 401 см2. Заряд пластин 1,42 мкКл. Найти напряжённость между пластинами.
3. Какова ёмкость и энергия конденсатора, если при его зарядке до напряжения 2 кВ он получает заряд 28 нКл?
Контрольные вопросы
1. Что называют конденсатором? Для чего они используются?
2. Из чего состоит плоский конденсатор?
3. Какую физическую величину называют электроёмкостью конденсатора?
4. Чему равна электроёмкость плоского конденсатора?
5. Перечислите формулы, с помощью которых можно определить энергию заряжённого конденсатора.
6. Чем обусловлена энергия конденсатора?
7. Как изменится напряжение между пластинами плоского конденсатора, если их немного раздвинуть, не изменяя заряд конденсатора?
Упражнение 1
1. 239 кВ/м
2. 4 МВ/м
3. 14 пФ, 28 мкДж
- Конденсаторы
- Электрическая ёмкость конденсатора
- Электроёмкость плоского конденсатора
- Энергия заряжённого конденсатора
- знать, что такое конденсатор
- знать, как определяется электрическая ёмкость конденсатора
- уметь рассчитывать электроёмкость плоского конденсатора
- уметь находить энергию заряжённого конденсатора различными способами
- Какие тела называют проводниками?
- Что такое диэлектрическая проницаемость вещества?
- Выполняется ли принцип суперпозиции для электрических сил?
Конденсаторы
Из курса физики 8 класса вам известно, что ток — это упорядоченное движение заряжённых частиц. Описанные ранее способы разделения разноимённо электрических зарядов — электризация при соприкосновении, электростатическая индукция — позволяют получить на поверхности тел лишь сравнительно небольшое число свободных электрических зарядов. В случае если потребуется накопление солидного количества разноимённых электрических зарядов, то применяется такой прибор, как конденсатор. Конденсаторы применяются в электронных, радиотехнических и электрических устройствах. Если вы разберете любой электроприбор, работающий не от сети, то обязательно встретите его там.
Конденсатор — система, состоящая из двух проводников (обкладок), разделённых слоем диэлектрика, толщина которого мала по сравнению с размерами проводников.
Плоский конденсатор — система, которая состоит из двух плоских параллельных пластин, заряжённых равными по модулю зарядами противоположного знака и разделённых слоем диэлектрика.
 Рис. 1. Напряжённость плоского конденсатора
Рис. 1. Напряжённость плоского конденсатора
При зарядке обкладкам конденсатора сообщают равные по модулю разноимённые заряды. Если пластинам плоского конденсатора сообщить равные по модулю заряды, но противоположные по знаку, то напряжённость электрического поля между пластинами будет в два раза больше, чем напряжённость электрического поля у одной пластины. Вне пластин напряжённость электрического поля равна нулю, так как равные заряды разного знака на двух пластинах создают вне пластин электрические поля, напряжённости которых равны по модулю, но противоположны по направлению (рис. 1). Отметим, что именно заряд положительно заряжённой пластины называют зарядом конденсатора.
Электрическая ёмкость конденсатора
Эксперименты показывают, что напряжение между пластинами конденсатора прямо пропорционально его заряду . Это позволяет ввести физическую величину, характеризующую способность конденсатора накапливать электрический заряд.
Отношение заряда конденсатора к модулю напряжения между его пластинами называют электрической ёмкостью конденсатора:
.
При неизменном расположении пластин электроёмкость конденсатора является постоянной величиной при любом заряде на пластинах.
Единица измерения ёмкости в СИ — фарад (Ф). Электроёмкостью в 1 Ф обладает такой конденсатор, напряжение которого равно 1 В при сообщении обкладкам разноимённых зарядов по 1 Кл.
Отметим, что 1 Ф — очень большая ёмкость, поэтому на практике широко используются дольные единицы электроёмкости — микрофарад (мкФ), нанофарад (нФ) и пикофарад (пФ):
1 мкФ = 10−6 Ф;
1 нФ = 10−9 Ф;
1 пФ = 10−12 Ф.
Электроёмкость плоского конденсатора
Напряжённость поля между двумя пластинами плоского конденсатора равна сумме напряжённостей полей, создаваемых каждой из пластин:
.
Если на пластинах площадью находятся электрические заряды и , то на основании известной формулы для напряжённости электрического поля бесконечной плоскости с поверхностной плотностью зарядов
 Рис. 2. Плоский конденсатор
Рис. 2. Плоский конденсатор
можно записать для модуля напряжённости поля между пластинами следующее выражение:
.
Для однородного электрического поля связь между напряжённостью и напряжением даётся выражением
,
где — в данном случае расстояние между пластинами, — напряжение на конденсаторе.
Подставим вышеизложенные формулы в выражение для электроёмкости конденсатора:
.
.
Энергия заряжённого конденсатора
Зарядим конденсатор и затем подключим к его выводам электрическую лампочку. При подключении лампочки в цепь наблюдается кратковременная вспышка света. Из этого опыта следует, что заряжённый конденсатор обладает энергией.
Если на обкладках конденсатора электроёмкостью находятся электрические разноимённые заряды и , то согласно выражению для электроёмкости напряжение между обкладками конденсатора можно выразить как
.
В процессе разрядки конденсатора напряжение между его обкладками убывает прямо пропорционально заряду от первоначального напряжения до 0. Среднее значение напряжения в процессе разрядки равно
.
Работа по переносу заряда между двумя точками в электростатическом поле пропорциональна разности потенциалов в этих двух точках. Тогда для работы , совершаемой электрическим полем при разрядке конденсатора, будем иметь следующий вид:
.
Таким образом, энергия электрического поля заряжённого конденсатора может найдена по следующим формулам
.
Наличие диэлектрика между пластинами конденсатора не изменит формулу для энергии электрического поля. Внесение диэлектрика между пластинами уменьшит напряжённость поля в раз. Тогда с учётом диэлектрика можно записать
.
Видно, что результат остаётся тем же. Также полученные формулы для расчёта энергии электрического поля заряжённого конденсатора справедливы не только для плоских конденсаторов, но и для конденсаторов любой формы.
Пример 1
Определите заряд и энергию электрического поля конденсатора ёмкостью = 5 нФ, если напряжение между его обкладками = 80 В.
Решение
1. Взаимосвязь между зарядом, ёмкостью и напряжением задаётся следующей формулой:
.
Отсюда найдём заряд:
.
2. Найдём энергию электрического поля конденсатора:
.
Ответ: , .
Упражнение 1
1. Напряжение между пластинами плоского воздушного конденсатора
= 239 В, а расстояние между ними = 1 мм. Определите напряжённость электрического поля между пластинами конденсатора.
2. Площадь каждой пластины плоского конденсатора 401 см2. Заряд пластин 1,42 мкКл. Найти напряжённость между пластинами.
3. Какова ёмкость и энергия конденсатора, если при его зарядке до напряжения 2 кВ он получает заряд 28 нКл?
Контрольные вопросы
1. Что называют конденсатором? Для чего они используются?
2. Из чего состоит плоский конденсатор?
3. Какую физическую величину называют электроёмкостью конденсатора?
4. Чему равна электроёмкость плоского конденсатора?
5. Перечислите формулы, с помощью которых можно определить энергию заряжённого конденсатора.
6. Чем обусловлена энергия конденсатора?
7. Как изменится напряжение между пластинами плоского конденсатора, если их немного раздвинуть, не изменяя заряд конденсатора?
Упражнение 1
1. 239 кВ/м
2. 4 МВ/м
3. 14 пФ, 28 мкДж



