- Метод подстановки в решении систем показательных уравнений
- Метод алгебраического сложения в решении систем показательных уравнений
- Решение системы, содержащей и показательное уравнение, и показательное неравенство
- Замена переменной при решении системы показательных уравнений
- Знать, как выглядят системы показательных уравнений и неравенств
- Уметь их решать методом подстановки, методом алгебраического сложения
1.Решить уравнение:
а) ; б) ; в) .
2. Решить неравенство:
а) ; б) .
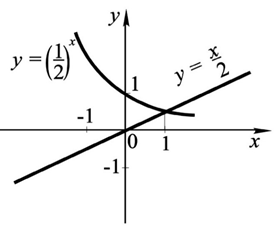
3. С помощью графиков решить неравенство:
а) ; б) .
Пример 1
Решить систему:
а)
б)
в)
г)
Решение
а)
Воспользуемся методом подстановки. Выразим из первого уравнения системы переменную x через y и подставим во второе уравнение:
Ответ: (3;2).
б)
Воспользуемся методом алгебраического сложения. Сложим почленно первое и второе уравнение системы, получим: , откуда x=1. Найденное значение переменной x подставим в первое уравнение:
Ответ: (1;4).
в)
Подставим y из второго уравнения системы в первое:
Найденные значения переменной x подставим во второе уравнение:
если x=2, то y=1,5; если x=1,5, то y=2. Так как по третьему условию системы разность x и y должна быть отрицательной, то x=1,5, y=2.
Ответ: (1,5; 2).
г)
Пусть . Тогда система уравнений примет вид:
Возведем второе уравнение системы во вторую степень при условии, что
, т.е. .
Подставим полученное выражение вместо переменной в первое уравнение:
Решим отдельно первое уравнение:
Подставим найденной значение V во второе уравнение:
Вернемся к исходным переменным: , . Значит, x=4, y=3.
Ответ: (4; 3).
Упражнение 1
Решить систему:
а) ;
б) ;
в) ;
Контрольный вопрос
- В чем заключается суть метода подстановки и метода алгебраического сложения при решении систем показательных уравнений и неравенств?
Упражнение 1
а) (1; 3); б) (2; -4); в) (0; 1).
- Метод подстановки в решении систем показательных уравнений
- Метод алгебраического сложения в решении систем показательных уравнений
- Решение системы, содержащей и показательное уравнение, и показательное неравенство
- Замена переменной при решении системы показательных уравнений
- Знать, как выглядят системы показательных уравнений и неравенств
- Уметь их решать методом подстановки, методом алгебраического сложения
1.Решить уравнение:
а) ; б) ; в) .
2. Решить неравенство:
а) ; б) .
3. С помощью графиков решить неравенство:
а) ; б) .

Пример 1
Решить систему:
а)
б)
в)
г)
Решение
а)
Воспользуемся методом подстановки. Выразим из первого уравнения системы переменную x через y и подставим во второе уравнение:
Ответ: (3;2).
б)
Воспользуемся методом алгебраического сложения. Сложим почленно первое и второе уравнение системы, получим: , откуда x=1. Найденное значение переменной x подставим в первое уравнение:
Ответ: (1;4).
в)
Подставим y из второго уравнения системы в первое:
Найденные значения переменной x подставим во второе уравнение:
если x=2, то y=1,5; если x=1,5, то y=2. Так как по третьему условию системы разность x и y должна быть отрицательной, то x=1,5, y=2.
Ответ: (1,5; 2).
г)
Пусть . Тогда система уравнений примет вид:
Возведем второе уравнение системы во вторую степень при условии, что
, т.е. .
Подставим полученное выражение вместо переменной в первое уравнение:
Решим отдельно первое уравнение:
Подставим найденной значение V во второе уравнение:
Вернемся к исходным переменным: , . Значит, x=4, y=3.
Ответ: (4; 3).
Упражнение 1
Решить систему:
а) ;
б) ;
в) ;
Контрольный вопрос
- В чем заключается суть метода подстановки и метода алгебраического сложения при решении систем показательных уравнений и неравенств?
Упражнение 1
а) (1; 3); б) (2; -4); в) (0; 1).



