- Введение арифметического корня натуральной степени
- Введение корня нечетной степени из отрицательного числа
- Перечисление основных свойств арифметического корня n-ой степени
- Решение задач на свойства арифметического корня n-ой степени
- Знать определение арифметического корня натуральной степени, свойства корня n-ой степени
- Уметь применять свойства корня n-ой степени при решении задач
1.Возвести в квадрат числа:
0; 6;
2. Представить в виде квадрата числа:
1;
3. Представить в виде куба числа:
4. Вычислить:
Решим графически уравнение .
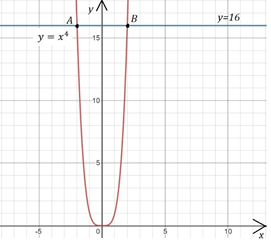
В одной и той же системе координат построим графики левой и правой частей уравнения, т.е. . Они пересекаются в двух точках
А и В . Их абсциссы являются решениями уравнения . Эти корни называются корнями четвертой степени из числа 16, а положительный корень (равный 2) называют арифметическим корнем четвертой степени из числа 16.
Вообще, при решении уравнения получается единственный неотрицательный корень. Он называется арифметическим корнем n-ой степени из числа a.
Арифметическим корнем натуральной степени из неотрицательного числа a называется неотрицательное число, n-ая степень которого равна a.
Обозначение: .
Выражение a называют подкоренным выражением.
В случае , в обозначении корня 2 не пишут, а пишут и называют «квадратный корень из числа a».
В случае , называют «кубический корень из числа a».
Решим уравнение .
Перенесем слагаемое из правой части в левую и разложим получившийся многочлен на множители . Если приравнять второй множитель к нулю, то дискриминант этого выражения будет отрицательным, значит для любого действительного x. Тогда . Получили, что уравнение имеет один действительный корень . Этот корень не является арифметическим, т.к. он отрицательный. Он называется кубическим корнем из числа -64 и обозначается : .
При решении уравнения в случае нечетности n и отрицательности a, т.е. при решении имеем только один отрицательный корень . Он называется корнем нечетной степени из отрицательного числа.
Так как .
Например, .
Операция нахождения корня n-й степени из неотрицательного числа является обратной к возведению в соответствующую степень и называется извлечением корня n-й степени.
Пример 1
Вычислить
Решение
Ответ:
Свойства арифметического корня n-ой степени
Пусть
- ;
- ;
- ;
- ;
- ;
- .
Вообще говоря, в свойстве 1 b может быть равным 0; в свойстве 3 в случае положительного значения a, m может быть любым целым.
Пример 2
Вычислить:
а) ;
б) ;
в) ;
г) ;
д) ;
е) .
Решение
а) ;
б) ;
в) ;
г) ;
д) ;
е)
.
Ответ: а) 2; б) ; в) ; г) 432; д) 0,5; е) 4.
Упражнение 1
Вычислить:
а) ;
б) ;
в);
г);
д)
Пример 3
Упростить выражения:
а) , при x>0, y>0,
б), при x>0, y>0.
Решение
а) ;
б) .
Ответ: а) ; б)
Упражнение 2
Упростить выражения:
а) , где ;
б), где .
Пример 4
Избавиться от иррациональности в знаменателе .
Решение
Умножим числитель и знаменатель дроби на выражение, сопряженное знаменателю, а именно на .
=.
Теперь умножим числитель и знаменатель дроби на .
.
Ответ: .
Упражнение 3
Избавиться от иррациональности в знаменателе .
Заметим, корень четной степени имеет смысл только на множестве неотрицательных чисел, корень нечетной степени определен для любого действительного числа.
Пример 5
При каких x выражение имеет смысл:
a)
б)
Решение
а) Так как дан корень четной кратности, то подкоренное выражение должно быть неотрицательным, т.е. . Решив это неравенство, получим
б) .
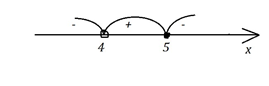
Ответ: а) б)(4;5]
Упражнение 4
При каких выражение имеет смысл:
а) ;
б) ;
в) .
Итак:
1. Арифметическим корнем натуральной степени из неотрицательного числа a называется неотрицательное число, n-ая степень которого равна a.
2. Решение уравнения называется корнем нечетной степени из отрицательного числа.
3. При .
4. Пусть
- ;
- ;
- ;
- ;
- .
5. .
Контрольные вопросы
- Что называют арифметическим корнем натуральной степени?
- Что называют корнем нечетной степени из неотрицательного числа?
- Какие свойства корня вы знаете?
- Найти область допустимых значений выражения: a) ; б).
Упражнение 1
а) ;
б) 3;
в) 5;
г) 162;
д) 6.
Упражнение 2
а) ;
б) .
Упражнение 3
Упражнение 5
- Введение арифметического корня натуральной степени
- Введение корня нечетной степени из отрицательного числа
- Перечисление основных свойств арифметического корня n-ой степени
- Решение задач на свойства арифметического корня n-ой степени
- Знать определение арифметического корня натуральной степени, свойства корня n-ой степени
- Уметь применять свойства корня n-ой степени при решении задач
1.Возвести в квадрат числа:
0; 6;
2. Представить в виде квадрата числа:
1;
3. Представить в виде куба числа:
4. Вычислить:
Решим графически уравнение .

В одной и той же системе координат построим графики левой и правой частей уравнения, т.е. . Они пересекаются в двух точках
А и В . Их абсциссы являются решениями уравнения . Эти корни называются корнями четвертой степени из числа 16, а положительный корень (равный 2) называют арифметическим корнем четвертой степени из числа 16.
Вообще, при решении уравнения получается единственный неотрицательный корень. Он называется арифметическим корнем n-ой степени из числа a.
Арифметическим корнем натуральной степени из неотрицательного числа a называется неотрицательное число, n-ая степень которого равна a.
Обозначение: .
Выражение a называют подкоренным выражением.
В случае , в обозначении корня 2 не пишут, а пишут и называют «квадратный корень из числа a».
В случае , называют «кубический корень из числа a».
Решим уравнение .
Перенесем слагаемое из правой части в левую и разложим получившийся многочлен на множители . Если приравнять второй множитель к нулю, то дискриминант этого выражения будет отрицательным, значит для любого действительного x. Тогда . Получили, что уравнение имеет один действительный корень . Этот корень не является арифметическим, т.к. он отрицательный. Он называется кубическим корнем из числа -64 и обозначается : .
При решении уравнения в случае нечетности n и отрицательности a, т.е. при решении имеем только один отрицательный корень . Он называется корнем нечетной степени из отрицательного числа.
Так как .
Например, .
Операция нахождения корня n-й степени из неотрицательного числа является обратной к возведению в соответствующую степень и называется извлечением корня n-й степени.
Пример 1
Вычислить
Решение
Ответ:
Свойства арифметического корня n-ой степени
Пусть
- ;
- ;
- ;
- ;
- ;
- .
Вообще говоря, в свойстве 1 b может быть равным 0; в свойстве 3 в случае положительного значения a, m может быть любым целым.
Пример 2
Вычислить:
а) ;
б) ;
в) ;
г) ;
д) ;
е) .
Решение
а) ;
б) ;
в) ;
г) ;
д) ;
е)
.
Ответ: а) 2; б) ; в) ; г) 432; д) 0,5; е) 4.
Упражнение 1
Вычислить:
а) ;
б) ;
в);
г);
д)
Пример 3
Упростить выражения:
а) , при x>0, y>0,
б), при x>0, y>0.
Решение
а) ;
б) .
Ответ: а) ; б)
Упражнение 2
Упростить выражения:
а) , где ;
б), где .
Пример 4
Избавиться от иррациональности в знаменателе .
Решение
Умножим числитель и знаменатель дроби на выражение, сопряженное знаменателю, а именно на .
=.
Теперь умножим числитель и знаменатель дроби на .
.
Ответ: .
Упражнение 3
Избавиться от иррациональности в знаменателе .
Заметим, корень четной степени имеет смысл только на множестве неотрицательных чисел, корень нечетной степени определен для любого действительного числа.
Пример 5
При каких x выражение имеет смысл:
a)
б)
Решение
а) Так как дан корень четной кратности, то подкоренное выражение должно быть неотрицательным, т.е. . Решив это неравенство, получим
б) .

Ответ: а) б)(4;5]
Упражнение 4
При каких выражение имеет смысл:
а) ;
б) ;
в) .
Итак:
1. Арифметическим корнем натуральной степени из неотрицательного числа a называется неотрицательное число, n-ая степень которого равна a.
2. Решение уравнения называется корнем нечетной степени из отрицательного числа.
3. При .
4. Пусть
- ;
- ;
- ;
- ;
- .
5. .
Контрольные вопросы
- Что называют арифметическим корнем натуральной степени?
- Что называют корнем нечетной степени из неотрицательного числа?
- Какие свойства корня вы знаете?
- Найти область допустимых значений выражения: a) ; б).
Упражнение 1
а) ;
б) 3;
в) 5;
г) 162;
д) 6.
Упражнение 2
а) ;
б) .
Упражнение 3
Упражнение 5



