- Введение в тему
- Последовательное построение алгоритма
- Разработка алгоритма методом последовательного уточнения для исполнителя Робот
- Вспомогательные алгоритмы
- научиться разрабатывать алгоритмы методом последовательного уточнения
- научиться строить вспомогательные алгоритмы для исполнителя Робот
- изучить, что собой представляют рекурсивные алгоритмы
- Что такое алгоритм?
- Какие существуют формы представления алгоритмов?
Введение в тему
Тему «Конструирование алгоритмов» составляют важные разделы информатики, знание которых позволяет лучше понимать процессы алгоритмизации и способствует осознанному изучению программирования.
Умение последовательно уточнять решение задачи способствует развитию алгоритмического мышления. Понимание вспомогательных алгоритмов поможет в решении сложных практических задач.
Последовательное построение алгоритма
Алгоритм — это понятное и точное предписание исполнителю выполнить определённый набор команд, приводящих к результату.
Исполнитель — это объект (живой организм (неформальный исполнитель) или техническое устройство (формальный исполнитель)), который выполняет заданный алгоритм.
Последовательное построение алгоритма — это метод конструирования алгоритмов, основанный на поэтапном уточнении конкретной задачи.
Другие названия метода последовательного построения алгоритма: «пошаговая детализация», «программирование сверху вниз», «нисходящее программирование».
Алгоритм метода последовательного построения алгоритма:
- Определение исходных данных и результатов, которые должны быть получены. На данном этапе считается, что исполнитель — это идеальный объект, который может решить любую задачу.
- Проверка выполнимости исполнителем конкретной задачи. Если исполнитель не может выдать ответ на задачу, то разбить задачу на несколько действий (частей). Если и теперь исполнитель снова не может выполнить поставленную задачу, нужно продолжить упрощение алгоритма — разбить части задачи на ещё более простые. Так нужно поступать до тех пор, пока все части задачи не станут понятны конкретному исполнителю.
- Объединение полученных частей задачи для получения алгоритма, решающего конкретную задачу.
Рассмотрим пример разработки алгоритма методом последовательного уточнения для исполнителя Робот.
Разработка алгоритма методом последовательного уточнения для исполнителя Робот
Исполнитель Робот — это формальный исполнитель, деятельность которого осуществляется на клетчатом поле, где он может перемещаться, обходя препятствия (стены).
Система команд исполнителя Робот в среде КуМир (комплект учебных миров) можно разделить на 2 группы:
1. Команды-действия (таблица 1).
Таблица 1. Команды-действия исполнителя Робот в среде КуМир

2. Команды-условия (таблица 2).
Таблица 2. Команды-условия исполнителя Робот в среде КуМир
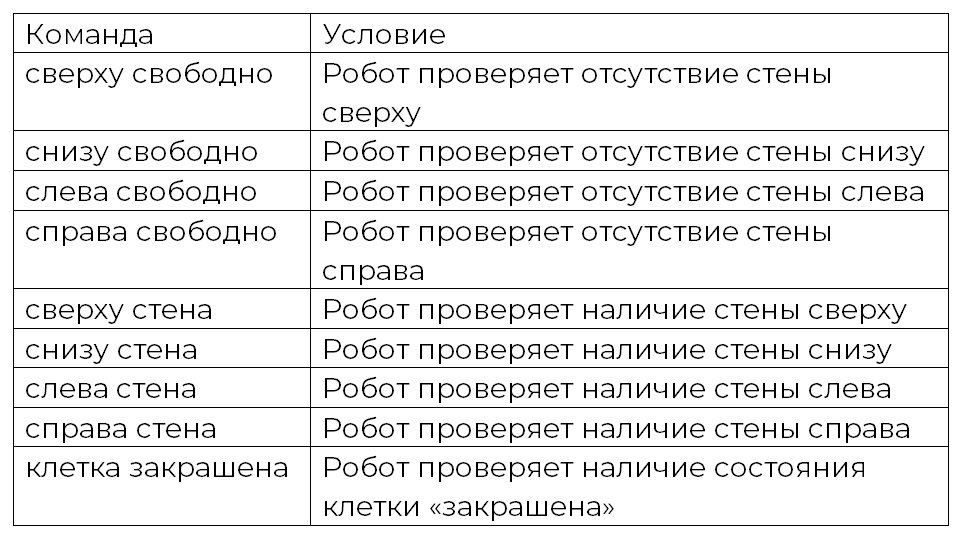
Реализация ветвлений:
1. Полное ветвление.
Общий вид конструкции полного ветвления:
если «условие»
то «команда 1»
иначе «команда 2»
все
2. Неполное ветвление.
Общий вид конструкции неполного ветвления:
если «условие»
то «команда»
все
Реализация циклов:
1. Цикл со счётчиком (применяется, когда заранее известно количество повторений).
Общий вид конструкции цикла со счётчиком:
нц «количество повторений» раз
«команда 1»
«команда 2»
…
«команда n»
кц
2. Цикл с условием (применяется для проверки истинности условия).
Общий вид конструкции цикла с условием:
нц пока «условие»
«последовательность команд»
кц
В одном условии можно применять несколько команд, используя логически связки И, ИЛИ, НЕ.
Рассмотрим пример разработки алгоритма методом последовательного уточнения для исполнителя Робот.
Задача 1
Имеется бесконечное клетчатое поле, размеры которого неизвестны. Внутри поля в произвольном месте располагаются две стены, соединённые под углом 90 градусов. Робот располагается в клетке, которая направлена вправо.
На рис. 1 показан возможный способ расположения стен и Робота (Робот обозначен ромбом).
Создайте алгоритм, закрашивающий все клетки, расположенные правее вертикальной стены, выше горизонтальной стены и примыкающие к ним, кроме угловой клетки. Например, для приведённого рисунка Робот должен закрасить следующие клетки (рис. 2).
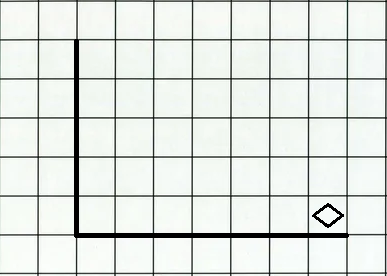 Рис. 1. Возможное расположение Робота и стен
Рис. 1. Возможное расположение Робота и стен
Конечное положение Робота — произвольное. Алгоритм должен решать задачу для произвольного размера поля и любого допустимого расположения стен внутри прямоугольного поля. При исполнении алгоритма Робот не должен разрушиться, выполнение алгоритма должно завершиться.
 Рис. 2. Пример результата выполнения программы Роботом
Рис. 2. Пример результата выполнения программы Роботом
Решение
1. Из условия задачи следует, что необходимо составить алгоритм, с помощью которого Робот пройдёт и закрасит только нужные клетки вдоль стен произвольной длины, без закрашивания угловой клетки.
Представим решение задачи линейным планом действий, предполагая, что исполнитель Робот является идеальным (рис. 3)
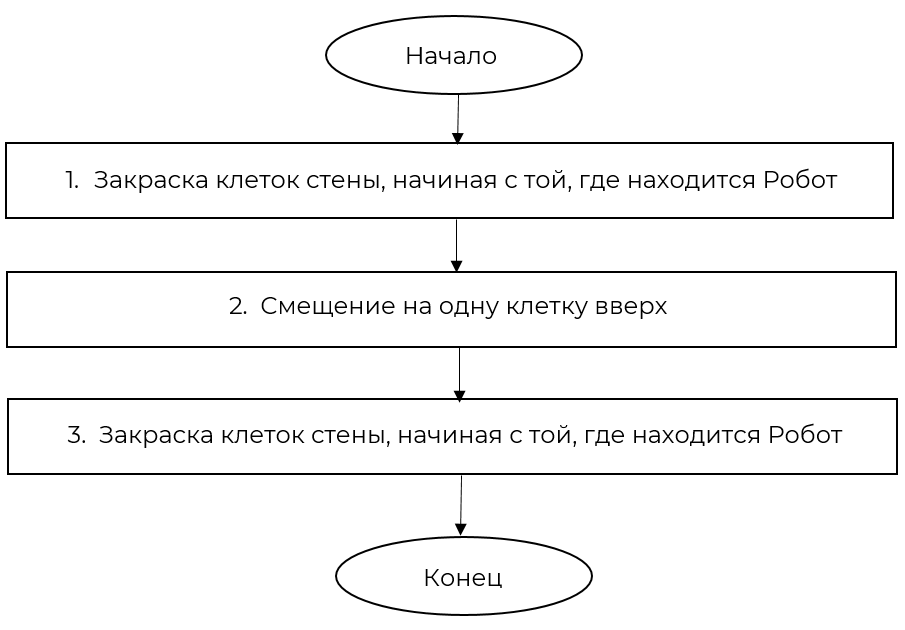 Рис. 3. Линейный алгоритм
Рис. 3. Линейный алгоритм
2. Начнём написание программы с операции Вставка -> использовать Робот (рис. 4)
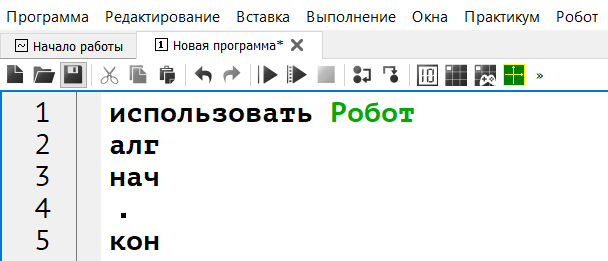 Рис. 4. Заготовка программы
Рис. 4. Заготовка программы
3. Создадим стартовую обстановку как на рис. 1 (Робот -> Редактировать стартовую обстановку). С помощью нажатия на границы ячеек расставим стены и переместим Робота на нужную позицию, взятую также из рис. 1. Созданную стартовую обстановку сохраним под названием Обстановка задания 1.fil (рис. 5).
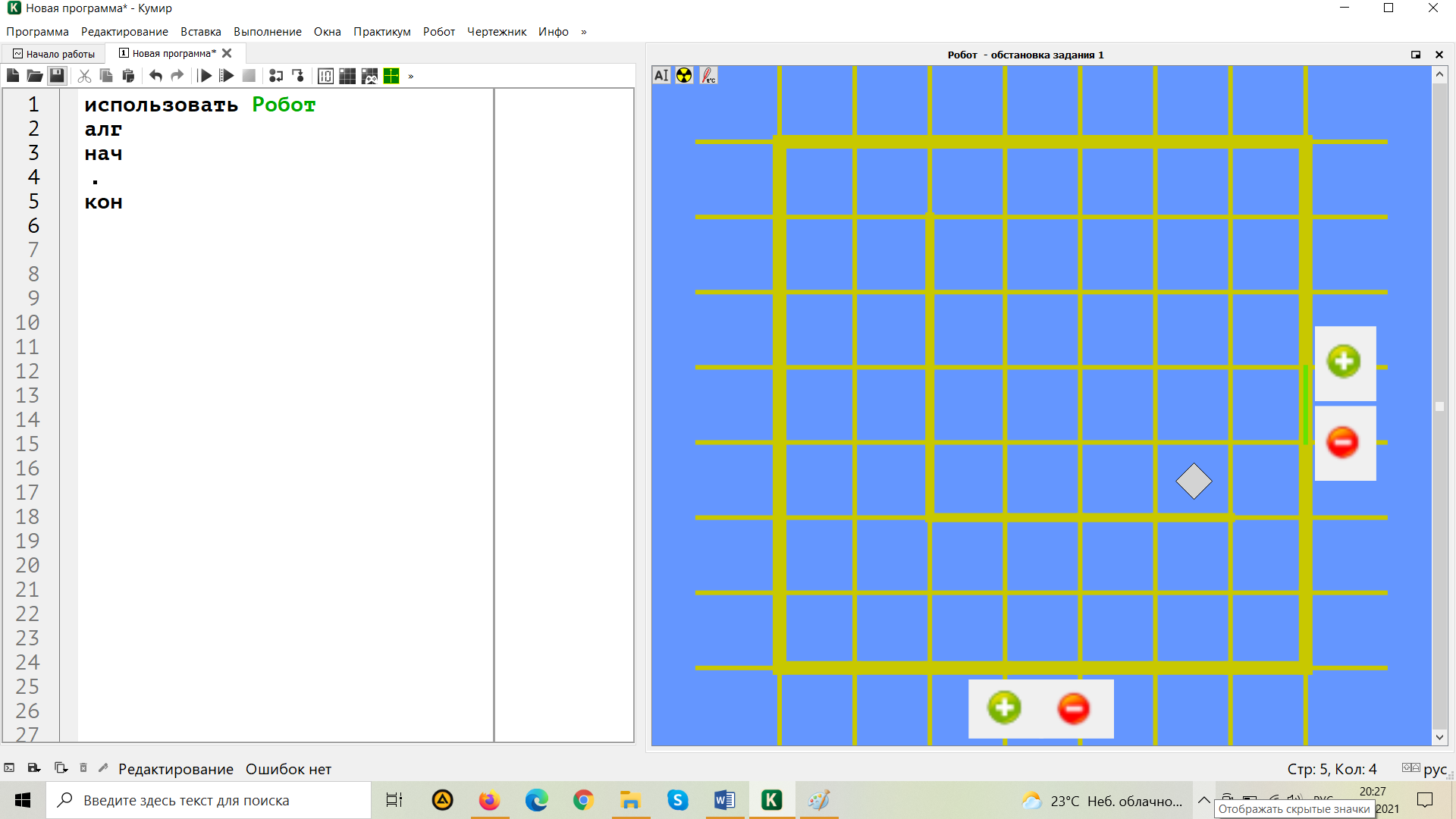 Рис. 5. Создание стартовой обстановки
Рис. 5. Создание стартовой обстановки
4. Выполним сохранение новой программы под названием Задание 1 в папку, где находится файл Обстановка задания 1.fil.
5. Детализируем все 3 пункта, описанные в рис. 3.
6. Чтобы закрасить все клетки стены, начиная с той, где находится Робот, необходимо проверять отсутствие стены слева, закрашивать клетку и перемещаться влево (рис. 6)
 Рис. 6. Закрашивание клеток стены
Рис. 6. Закрашивание клеток стены
7. Смещение на одну клетку вверх вне цикла позволит осуществить переход без закрашивания клетки (рис. 7).
 Рис. 7. Пропуск одной незакрашенной клетки (вне цикла)
Рис. 7. Пропуск одной незакрашенной клетки (вне цикла)
8. Теперь проверим несвободность слева, закрасим и сместимся вверх (рис. 8)
 Рис. 8. Закраска вертикальной стены
Рис. 8. Закраска вертикальной стены
Вся программа представлена на рис. 9
 Рис. 9. Программа к задаче 1
Рис. 9. Программа к задаче 1
Пример работы программы представлен на рис. 10.
 Рис. 10. Пример работы программы к задаче 1
Рис. 10. Пример работы программы к задаче 1
Чтобы подобные программы работали корректно, следует загружать нужные стартовые обстановки (Робот -> Загрузить обстановку).
Вспомогательные алгоритмы
Вспомогательный алгоритм (подпрограмма) — это алгоритм, целиком применяемый другим алгоритмом.
Рассмотрим пример написания вспомогательного алгоритма для исполнителя Робот.
Задача 2
Создать программу для исполнителя Робот с использованием вспомогательного алгоритма Узор (рис. 11).
 Рис. 11. Рисунок к условию задачи 2
Рис. 11. Рисунок к условию задачи 2
Решение
1. Чтобы наглядно показать отличия программы, написанной с использованием вспомогательного алгоритма и без неё, сравним две программы.
2. Программа, написанная без использования вспомогательного алгоритма (рис. 12).
 Рис. 12. Программа без вспомогательного алгоритма
Рис. 12. Программа без вспомогательного алгоритма
3. Программа, написанная с использованием вспомогательного алгоритма (рис. 13).
 Рис. 13. Программа с вспомогательным алгоритмом
Рис. 13. Программа с вспомогательным алгоритмом
Главные отличия вспомогательных алгоритмов, используемых для исполнителя Робот:
- Вспомогательный алгоритм имеет большую часть признаков программы (есть алг, нач, кон).
- Вспомогательный алгоритм имеет имя, по которому к нему обращаются в основной программе.
Рекурсивный алгоритм — это алгоритм, вызывающий себя непосредственно или через другие алгоритмы.
Для простого примера рекурсию можно представить следующим образом
(рис. 14).
 Рис. 14. Наглядный пример рекурсии
Рис. 14. Наглядный пример рекурсии
Рассмотрим пример задачи, которую можно решить построением рекурсивного алгоритма.
Решение
1. Известно, что факториал вычисляется путём умножения всех чисел от одного до значения самого числа под факториалом.
2. В нашем случае, чтобы найти 5!, можно записать следующее решение:
1! = 1,
2! = 1 × 2 = 2,
3! = 1 × 2 × 3 = 6,
4! = 1 × 2 × 3 × 4 = 24,
5! = 1 × 2 × 3 × 4 × 5 = 120.
3. Граф, представленный на рис. 15, — процесс решения задачи, описанный в пункте 2.
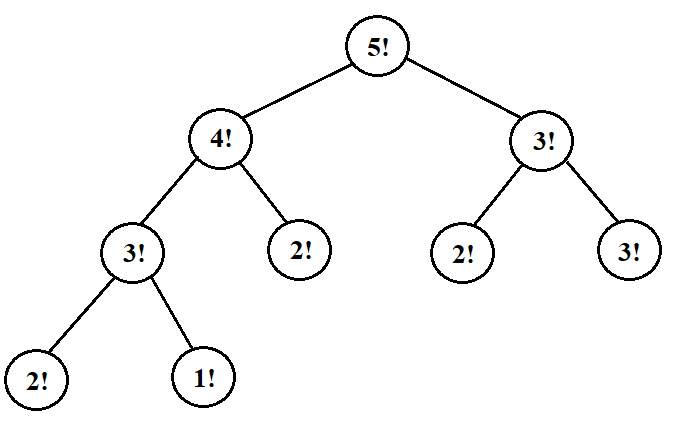 Рис. 15. Дерево решений факториала 5!
Рис. 15. Дерево решений факториала 5!
4. Представим решение задачи с помощью блок-схемы (рис. 16).
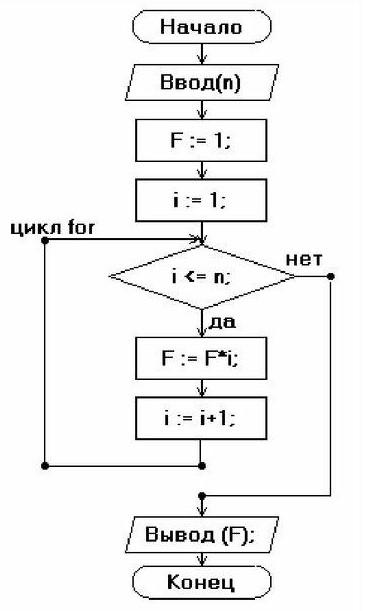 Рис. 16. Блок-схема решения задачи 2
Рис. 16. Блок-схема решения задачи 2
В дальнейшем, опираясь на блок-схему, можно написать программу для нахождения факториала числа.
Контрольные вопросы
- Перечислите команды-действия исполнителя Робот в среде КуМир.
- Перечислите команды-условия исполнителя Робот в среде КуМир.
- Чем отличается конструкция полного ветвления от неполного ветвления?
- В чём заключается принципиальное отличие цикла со счётчиком от цикла с условием? В каких случаях следует применить каждый из них?
- Какой алгоритм называется рекурсивным? Когда следует применять рекурсивный алгоритм?

