- Конденсаторы
- Энергия электрического поля конденсатора
- знать формулы для расчёта напряжения между пластинами конденсатора; формулы для расчёта энергии электрического поля конденсатора; от чего зависит ёмкость конденсатора
- уметь выводить формулы для расчёта энергии электрического поля конденсатора
- По какой формуле рассчитывается работа электрического поля?
- Что такое конденсатор?
- Как выглядит картина силовых линий двух противоположно заряженных пластин?
Конденсаторы
Конденсатор представляет собой прибор для накопления электрического заряда, он состоит из двух металлических проводников, изолированных друг от друга. Проводники, из которых изготовлен конденсатор, называются обкладками конденсатора.
Чаще всего встречаются конденсаторы трёх видов: плоские, цилиндрические и сферические (рис. 1).
Плоский конденсатор состоит из двух параллельных пластин, при этом расстояние между пластинами много меньше размеров самих пластин. Пространство между обкладками заполнено воздухом (воздушный конденсатор) или другим диэлектриком.
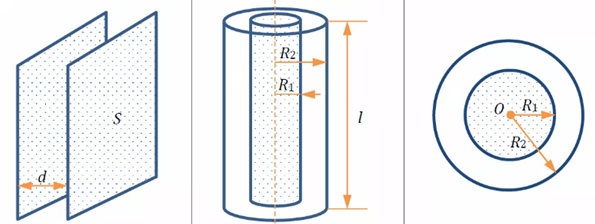 Рис. 1. Виды конденсаторов
Рис. 1. Виды конденсаторов
Существуют цилиндрические конденсаторы, в которых обкладки имеют форму цилиндров разного размера. Цилиндры вставлены один в другой и разделены слоем диэлектрика. Аналогично устроены сферические конденсаторы, которые представляют собой систему из двух сфер, сфера меньшего диаметра находится внутри большей сферы.
Когда конденсатор заряжен, напряжённость в пространстве вокруг конденсатора стремится к нулю. Практически вся электрическая энергия сосредоточена между обкладками.
Если конденсатор плоский и пластины заряжены одинаковыми по модулю, но противоположными зарядами, электрическое поле между обкладками будет однородным.
Заряд конденсатора принято брать равным заряду положительно заряженной пластины конденсатора. Напряжение между обкладками плоского конденсатора можно найти по следующей формуле:
,
где U [В] — напряжение между пластинами конденсатора;
E [В/м] — напряжённость однородного поля внутри конденсатора;
d [м] — расстояние между обкладками.
Очевидно, что чем сильнее заряжен конденсатор, тем больше модуль напряжённости между пластинами, тем больше значение напряжения.
Напряжение между обкладками зависит не только от заряда, переданного конденсатору, оно также зависит от характеристик самого прибора: площади пластин S, расстояния между обкладками d и вещества, заполняющего пространство между обкладками.
Перечисленные характеристики прибора определяют ёмкость конденсатора С. Тогда коэффициентом пропорциональности между приложенным напряжением и накопившемся на данном конденсаторе заряде является ёмкость. Напряжение прямо пропорционально его заряду и обратно пропорционально ёмкости конденсатора:
,
где q [Кл] — заряд конденсатора;
C [Ф] — ёмкость конденсатора.
В СИ емкость конденсатора измеряется в фарадах (Ф).
ёмкость конденсатора С прямо пропорциональна площади пластин S и обратно пропорциональна расстоянию между обкладками конденсатора d:
.
Пространство между пластинами конденсатора может быть заполнено диэлектриком: это может быть бумага, слюда или пластмассовая плёнка. Наличие диэлектрика увеличивает ёмкость конденсатора.
Добавление диэлектрика в пространство между обкладками конденсатора приводит к увеличению ёмкости конденсатора.
ёмкость конденсатора С зависит только от характеристик прибора: площади пластин, расстояния между ними, наличия диэлектрика и не зависит от напряжения и заряда конденсатора.
Энергия электрического поля конденсатора
Пластины конденсатора имеют противоположные заряды, следовательно, между ними возникают электрические силы притяжения (рис. 2), поэтому заряженный конденсатор всегда обладает энергией.
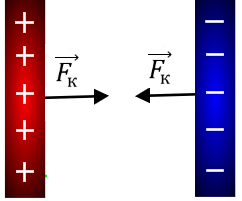 Рис. 2. Электрические силы в плоском конденсаторе
Рис. 2. Электрические силы в плоском конденсаторе
Представим, что положительно заряженная пластина 1 жёстко закреплена, а пластина 2, отрицательно заряженная, может свободно изменять своё положение. Тогда пластина 2 под действием силы Кулона притянется к первой, при этом поле первой пластины совершит положительную работу. После соединения пластин часть электронов с отрицательно заряженной пластины перейдёт на положительно заряженную пластину. Заряд распределится поровну, и в результате заряды обеих обкладок станут равны нулю.
Такая система не может совершать работу, конденсатор в этом случае не заряжен, энергия разряженного конденсатора равна нулю.
До того момента, когда пластины соприкоснулись, конденсатор обладал энергией, равной работе электрических сил при перемещении движущейся пластины.
Работа электрических сил определяется следующей формулой:
.
Сила электрического поля, с которой пластина 1 действует на пластину 2, находится как произведение напряжённости на заряд:
.
В данном случае q — заряд движущейся пластины 2; Е1 — напряжённость первой пластины.
Так как в заряженном конденсаторе заряды пластин численно равны, модули напряжённостей каждой из обкладок также равны Е1 = Е2. Суммарная напряжённость между пластинами Е, согласно принципу суперпозиции, складывается из напряжённостей каждого из заряженных тел: Е = Е1 + Е2. Следовательно, напряжённость каждой из пластин равна Е1 = Е2 = Е/2.
Тогда формула для определения работы электрических сил принимает следующий вид:
.
Учтём, что по формуле для напряжения между обкладками плоского конденсатора произведение напряжённости Е на расстояние между пластинами d равно напряжению:
.
Энергия электрического поля конденсатора W равна работе электрических сил:
.
Используя соотношение , выражение для энергии конденсатора можно преобразовать следующим образом:
,
где W [Дж] — энергия конденсатора;
C [Ф] — ёмкость конденсатора;
U [В] — напряжение межу обкладками;
q [Кл] — заряд конденсатора.
Данную формулу можно применять не только для расчёта энергии плоского конденсатора, она будет верна для расчёта конденсаторов любой формы.
Пример 1
К плоскому конденсатору ёмкостью 10 мкФ приложено напряжение U = 5 B. Чему равна напряжённость и энергия электрического поля между пластинами этого конденсатора, если пластины находятся на расстоянии 20 см друг от друга.
Решение
1. Запишем исходные данные:
U = 5 B; C = 10 мкФ = 10-5 Ф; d = 20 см = 0,2 м.
2. Найдём напряжённость электрического поля по следующей формуле:
.
3. Энергию найдём через ёмкость и напряжение конденсатора:
.
Ответ: ; .
Итоги
- Конденсатор представляет собой прибор для накопления электрического заряда, это система из двух металлических проводников, изолированных друг от друга слоем диэлектрика.
- Напряжение между обкладками конденсатора прямо пропорционально его заряду и обратно пропорционально ёмкости конденсатора: .
- ёмкость конденсатора С прямо пропорциональна площади пластин S и обратно пропорциональна расстоянию между обкладками конденсатора d. Добавление диэлектрика в пространство между пластинами конденсатора приводит к увеличению ёмкости конденсатора.
- Энергию конденсатора можно найти по одной из следующих формул: .
Контрольные вопросы
1. Как можно изменить напряжение на конденсаторе?
2. От каких характеристик зависит ёмкость конденсатора?
3. Назовите три формулы, по которым можно рассчитать энергию конденсатора.
- Конденсаторы
- Энергия электрического поля конденсатора
- знать формулы для расчёта напряжения между пластинами конденсатора; формулы для расчёта энергии электрического поля конденсатора; от чего зависит ёмкость конденсатора
- уметь выводить формулы для расчёта энергии электрического поля конденсатора
- По какой формуле рассчитывается работа электрического поля?
- Что такое конденсатор?
- Как выглядит картина силовых линий двух противоположно заряженных пластин?
Конденсаторы
Конденсатор представляет собой прибор для накопления электрического заряда, он состоит из двух металлических проводников, изолированных друг от друга. Проводники, из которых изготовлен конденсатор, называются обкладками конденсатора.
Чаще всего встречаются конденсаторы трёх видов: плоские, цилиндрические и сферические (рис. 1).
Плоский конденсатор состоит из двух параллельных пластин, при этом расстояние между пластинами много меньше размеров самих пластин. Пространство между обкладками заполнено воздухом (воздушный конденсатор) или другим диэлектриком.
 Рис. 1. Виды конденсаторов
Рис. 1. Виды конденсаторов
Существуют цилиндрические конденсаторы, в которых обкладки имеют форму цилиндров разного размера. Цилиндры вставлены один в другой и разделены слоем диэлектрика. Аналогично устроены сферические конденсаторы, которые представляют собой систему из двух сфер, сфера меньшего диаметра находится внутри большей сферы.
Когда конденсатор заряжен, напряжённость в пространстве вокруг конденсатора стремится к нулю. Практически вся электрическая энергия сосредоточена между обкладками.
Если конденсатор плоский и пластины заряжены одинаковыми по модулю, но противоположными зарядами, электрическое поле между обкладками будет однородным.
Заряд конденсатора принято брать равным заряду положительно заряженной пластины конденсатора. Напряжение между обкладками плоского конденсатора можно найти по следующей формуле:
,
где U [В] — напряжение между пластинами конденсатора;
E [В/м] — напряжённость однородного поля внутри конденсатора;
d [м] — расстояние между обкладками.
Очевидно, что чем сильнее заряжен конденсатор, тем больше модуль напряжённости между пластинами, тем больше значение напряжения.
Напряжение между обкладками зависит не только от заряда, переданного конденсатору, оно также зависит от характеристик самого прибора: площади пластин S, расстояния между обкладками d и вещества, заполняющего пространство между обкладками.
Перечисленные характеристики прибора определяют ёмкость конденсатора С. Тогда коэффициентом пропорциональности между приложенным напряжением и накопившемся на данном конденсаторе заряде является ёмкость. Напряжение прямо пропорционально его заряду и обратно пропорционально ёмкости конденсатора:
,
где q [Кл] — заряд конденсатора;
C [Ф] — ёмкость конденсатора.
В СИ емкость конденсатора измеряется в фарадах (Ф).
ёмкость конденсатора С прямо пропорциональна площади пластин S и обратно пропорциональна расстоянию между обкладками конденсатора d:
.
Пространство между пластинами конденсатора может быть заполнено диэлектриком: это может быть бумага, слюда или пластмассовая плёнка. Наличие диэлектрика увеличивает ёмкость конденсатора.
Добавление диэлектрика в пространство между обкладками конденсатора приводит к увеличению ёмкости конденсатора.
ёмкость конденсатора С зависит только от характеристик прибора: площади пластин, расстояния между ними, наличия диэлектрика и не зависит от напряжения и заряда конденсатора.
Энергия электрического поля конденсатора
Пластины конденсатора имеют противоположные заряды, следовательно, между ними возникают электрические силы притяжения (рис. 2), поэтому заряженный конденсатор всегда обладает энергией.
 Рис. 2. Электрические силы в плоском конденсаторе
Рис. 2. Электрические силы в плоском конденсаторе
Представим, что положительно заряженная пластина 1 жёстко закреплена, а пластина 2, отрицательно заряженная, может свободно изменять своё положение. Тогда пластина 2 под действием силы Кулона притянется к первой, при этом поле первой пластины совершит положительную работу. После соединения пластин часть электронов с отрицательно заряженной пластины перейдёт на положительно заряженную пластину. Заряд распределится поровну, и в результате заряды обеих обкладок станут равны нулю.
Такая система не может совершать работу, конденсатор в этом случае не заряжен, энергия разряженного конденсатора равна нулю.
До того момента, когда пластины соприкоснулись, конденсатор обладал энергией, равной работе электрических сил при перемещении движущейся пластины.
Работа электрических сил определяется следующей формулой:
.
Сила электрического поля, с которой пластина 1 действует на пластину 2, находится как произведение напряжённости на заряд:
.
В данном случае q — заряд движущейся пластины 2; Е1 — напряжённость первой пластины.
Так как в заряженном конденсаторе заряды пластин численно равны, модули напряжённостей каждой из обкладок также равны Е1 = Е2. Суммарная напряжённость между пластинами Е, согласно принципу суперпозиции, складывается из напряжённостей каждого из заряженных тел: Е = Е1 + Е2. Следовательно, напряжённость каждой из пластин равна Е1 = Е2 = Е/2.
Тогда формула для определения работы электрических сил принимает следующий вид:
.
Учтём, что по формуле для напряжения между обкладками плоского конденсатора произведение напряжённости Е на расстояние между пластинами d равно напряжению:
.
Энергия электрического поля конденсатора W равна работе электрических сил:
.
Используя соотношение , выражение для энергии конденсатора можно преобразовать следующим образом:
,
где W [Дж] — энергия конденсатора;
C [Ф] — ёмкость конденсатора;
U [В] — напряжение межу обкладками;
q [Кл] — заряд конденсатора.
Данную формулу можно применять не только для расчёта энергии плоского конденсатора, она будет верна для расчёта конденсаторов любой формы.
Пример 1
К плоскому конденсатору ёмкостью 10 мкФ приложено напряжение U = 5 B. Чему равна напряжённость и энергия электрического поля между пластинами этого конденсатора, если пластины находятся на расстоянии 20 см друг от друга.
Решение
1. Запишем исходные данные:
U = 5 B; C = 10 мкФ = 10-5 Ф; d = 20 см = 0,2 м.
2. Найдём напряжённость электрического поля по следующей формуле:
.
3. Энергию найдём через ёмкость и напряжение конденсатора:
.
Ответ: ; .
Итоги
- Конденсатор представляет собой прибор для накопления электрического заряда, это система из двух металлических проводников, изолированных друг от друга слоем диэлектрика.
- Напряжение между обкладками конденсатора прямо пропорционально его заряду и обратно пропорционально ёмкости конденсатора: .
- ёмкость конденсатора С прямо пропорциональна площади пластин S и обратно пропорциональна расстоянию между обкладками конденсатора d. Добавление диэлектрика в пространство между пластинами конденсатора приводит к увеличению ёмкости конденсатора.
- Энергию конденсатора можно найти по одной из следующих формул: .
Контрольные вопросы
1. Как можно изменить напряжение на конденсаторе?
2. От каких характеристик зависит ёмкость конденсатора?
3. Назовите три формулы, по которым можно рассчитать энергию конденсатора.

