- Простые механизмы
- Неподвижный блок
- Подвижный блок
- узнать, что такое простые механизмы
- узнать свойства неподвижного и подвижного блока
- узнать, что такое коэффициент полезного действия
- познакомиться с «золотым правилом механики»
- Почему не вся потраченная энергия может пойти на совершение работы?
Простые механизмы
В прошлой главе мы познакомились с рычагами первого и второго рода. Рычаг — это первый простой механизм, который изобрёл человек и который дал выигрыш в силе. Но были придуманы и другие простые механизмы, более удобные, которые дали не только выигрыш в силе, но и позволили изменить направление приложения силы.
Механические устройства, с помощью которых можно изменять направление и модуль силы, называют простыми механизмами.
Рассмотрим здесь подробно два вида простых механизмов — неподвижные и подвижные блоки. Блок представляет собой колесо с желобом, по которому пропускают верёвку, трос или цепь. Если ось вращения блока неподвижна (жёстко закреплена), то блок называют неподвижным. Если ось может перемещаться, то это — подвижный блок (рис. 1).
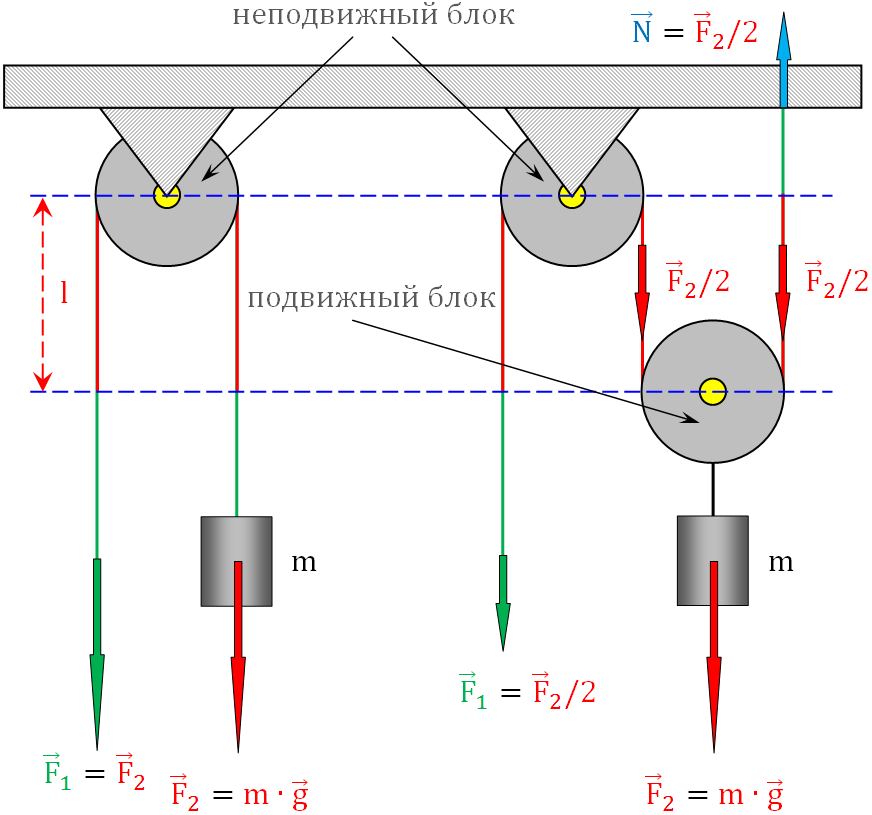 Рис. 1. Силы в системе с неподвижным и подвижным блоками
Рис. 1. Силы в системе с неподвижным и подвижным блоками
Неподвижный блок
Пусть через неподвижный блок перекинута нить, к правому концу которой подвешен груз массой m (рис. 1). Тогда справа на нить действует сила веса груза . Поскольку нить не изменяет приложенной к ней силы, а изменяет только её направление, то для удержания груза нужно приложить к левому концу нити силу . Таким образом, неподвижный блок не даёт выигрыша в силе, но позволяет изменить направление действия силы.
Чтобы поднять неподвижным блоком груз на высоту , нужно вытянуть нить на ту же длину . Следовательно, неподвижный блок не даёт выигрыша или проигрыша в расстоянии.
Для подъёма груза на высоту нужно совершить работу против силы тяжести:
.
Эта работа в точности равна работе силы, приложенной к левому концу нити, так как силы () и перемещения ( = ) совпадают:
.
Равенство работ является следствием закона сохранения энергии.
Итак, неподвижный блок не даёт выигрыша или проигрыша ни в силе, ни в расстоянии.
Подвижный блок
Пусть теперь груз массой m подвешен к невесомому подвижному блоку (рис. 1). Нить, на которой подвешен подвижный блок, соединена правым концом со стеной, а её левый конец удерживается силой , так что вся система находится в равновесии. На подвижный блок действует сила тяжести груза . Поскольку подвижный блок висит на двух нитях, то вес груза поровну делится между ними, т. е. силы натяжения нитей равны . Правый конец нити закреплён в стене и удерживается силой реакции стены равной по модулю . Сила передаётся от левой нити через неподвижный блок без изменения левому концу нити. Значит, для удержания груза нужна сила . Следовательно, подвижный блок даёт выигрыш в силе в 2 раза.
Чтобы поднять груз на высоту , необходимо совершить работу против силы тяжести:
.
Придётся вытянуть слева двойную длину нити , но тянуть с силой . Значит, подвижный блок даёт проигрыш в расстоянии в 2 раза.
Работа силы, приложенной к левому концу нити, равна
.
Как и в случае с неподвижным блоком, мы получили равенство работ, т. к. закон сохранения энергии справедлив и здесь. Равенство работ получилось благодаря тому, что двукратное уменьшение силы было компенсировано двукратным ростом перемещения.
Итак, подвижный блок даёт выигрыш в силе в 2 раза и проигрыш в расстоянии 2 раза.
В общем случае можно составить механизмы, которые дают любой выигрыш в силе, например, в 4 или 10 раз. Но закон сохранения энергии приведёт к тому, что во столько же раз, например, в 4 или 10, мы проиграем в расстоянии. Так мы пришли к формулировке «золотого правила механики».
Золотое правило механики: во сколько раз мы выигрываем в силе, во столько же раз проигрываем в расстоянии и наоборот.
В реальных механизмах работа по подъёму груза (или другая полезная работа) всегда будет меньше затраченной работы. Затраченная работа больше, т. к. приходится совершать работу против силы трения в узлах механизмов.
Отношение полезной работы к затраченной работе называют коэффициентом полезного действия (КПД) механизма: .
КПД обозначают греческой буквой (читается «эта») и выражают в долях или процентах. Поскольку в идеальном случае вся затраченная энергия идёт на совершение работы, то КПД идеального механизма будет равен 1 или 100 %. КПД реальных механизмов заметно меньше (табл. 1)
Таблица 1. КПД различных двигателей
|
Тип двигателя
|
КПД, %
|
|
Паровая машина
|
8–10
|
|
Двигатель внутреннего сгорания
|
20–25
|
|
Газовая турбина
|
25–30
|
|
Дизельный двигатель
|
40–45
|
|
Ракетный двигатель
|
47
|
Итоги
- Механические устройства, с помощью которых можно изменять направление и модуль силы, называют простыми механизмами.
- Неподвижный блок не даёт выигрыша или проигрыша ни в силе, ни в расстоянии.
- Подвижный блок даёт выигрыш в силе в 2 раза и проигрыш в расстоянии 2 раза.
- Золотое правило механики: во сколько раз мы выигрываем в силе, во столько же раз проигрываем в расстоянии и наоборот.
- Отношение полезной работы к затраченной работе называют коэффициентом полезного действия (КПД) механизма: .
Упражнение 1
1. При подъёме груза массой 100 кг на высоту 3 м с помощью механизма была затрачена работа 3 200 Дж. Чему равно КПД этого механизма?
Контрольные вопросы
1. Что такое простые механизмы?
2. Какие виды блоков вы знаете?
3. В чём состоит «золотое правило механики»?
4. Продемонстрируйте справедливость золотого правила механики на примере работы подвижного и неподвижного блоков.
5. Что такое КПД механизма?
6. Может ли КПД быть равным 2?
7. Что означает, что КПД равно 80 %?
Упражнение 1
1. КПД = 0,94 или 94 %.
- Простые механизмы
- Неподвижный блок
- Подвижный блок
- узнать, что такое простые механизмы
- узнать свойства неподвижного и подвижного блока
- узнать, что такое коэффициент полезного действия
- познакомиться с «золотым правилом механики»
- Почему не вся потраченная энергия может пойти на совершение работы?
Простые механизмы
В прошлой главе мы познакомились с рычагами первого и второго рода. Рычаг — это первый простой механизм, который изобрёл человек и который дал выигрыш в силе. Но были придуманы и другие простые механизмы, более удобные, которые дали не только выигрыш в силе, но и позволили изменить направление приложения силы.
Механические устройства, с помощью которых можно изменять направление и модуль силы, называют простыми механизмами.
Рассмотрим здесь подробно два вида простых механизмов — неподвижные и подвижные блоки. Блок представляет собой колесо с желобом, по которому пропускают верёвку, трос или цепь. Если ось вращения блока неподвижна (жёстко закреплена), то блок называют неподвижным. Если ось может перемещаться, то это — подвижный блок (рис. 1).
 Рис. 1. Силы в системе с неподвижным и подвижным блоками
Рис. 1. Силы в системе с неподвижным и подвижным блоками
Неподвижный блок
Пусть через неподвижный блок перекинута нить, к правому концу которой подвешен груз массой m (рис. 1). Тогда справа на нить действует сила веса груза . Поскольку нить не изменяет приложенной к ней силы, а изменяет только её направление, то для удержания груза нужно приложить к левому концу нити силу . Таким образом, неподвижный блок не даёт выигрыша в силе, но позволяет изменить направление действия силы.
Чтобы поднять неподвижным блоком груз на высоту , нужно вытянуть нить на ту же длину . Следовательно, неподвижный блок не даёт выигрыша или проигрыша в расстоянии.
Для подъёма груза на высоту нужно совершить работу против силы тяжести:
.
Эта работа в точности равна работе силы, приложенной к левому концу нити, так как силы () и перемещения ( = ) совпадают:
.
Равенство работ является следствием закона сохранения энергии.
Итак, неподвижный блок не даёт выигрыша или проигрыша ни в силе, ни в расстоянии.
Подвижный блок
Пусть теперь груз массой m подвешен к невесомому подвижному блоку (рис. 1). Нить, на которой подвешен подвижный блок, соединена правым концом со стеной, а её левый конец удерживается силой , так что вся система находится в равновесии. На подвижный блок действует сила тяжести груза . Поскольку подвижный блок висит на двух нитях, то вес груза поровну делится между ними, т. е. силы натяжения нитей равны . Правый конец нити закреплён в стене и удерживается силой реакции стены равной по модулю . Сила передаётся от левой нити через неподвижный блок без изменения левому концу нити. Значит, для удержания груза нужна сила . Следовательно, подвижный блок даёт выигрыш в силе в 2 раза.
Чтобы поднять груз на высоту , необходимо совершить работу против силы тяжести:
.
Придётся вытянуть слева двойную длину нити , но тянуть с силой . Значит, подвижный блок даёт проигрыш в расстоянии в 2 раза.
Работа силы, приложенной к левому концу нити, равна
.
Как и в случае с неподвижным блоком, мы получили равенство работ, т. к. закон сохранения энергии справедлив и здесь. Равенство работ получилось благодаря тому, что двукратное уменьшение силы было компенсировано двукратным ростом перемещения.
Итак, подвижный блок даёт выигрыш в силе в 2 раза и проигрыш в расстоянии 2 раза.
В общем случае можно составить механизмы, которые дают любой выигрыш в силе, например, в 4 или 10 раз. Но закон сохранения энергии приведёт к тому, что во столько же раз, например, в 4 или 10, мы проиграем в расстоянии. Так мы пришли к формулировке «золотого правила механики».
Золотое правило механики: во сколько раз мы выигрываем в силе, во столько же раз проигрываем в расстоянии и наоборот.
В реальных механизмах работа по подъёму груза (или другая полезная работа) всегда будет меньше затраченной работы. Затраченная работа больше, т. к. приходится совершать работу против силы трения в узлах механизмов.
Отношение полезной работы к затраченной работе называют коэффициентом полезного действия (КПД) механизма: .
КПД обозначают греческой буквой (читается «эта») и выражают в долях или процентах. Поскольку в идеальном случае вся затраченная энергия идёт на совершение работы, то КПД идеального механизма будет равен 1 или 100 %. КПД реальных механизмов заметно меньше (табл. 1)
Таблица 1. КПД различных двигателей
|
Тип двигателя
|
КПД, %
|
|
Паровая машина
|
8–10
|
|
Двигатель внутреннего сгорания
|
20–25
|
|
Газовая турбина
|
25–30
|
|
Дизельный двигатель
|
40–45
|
|
Ракетный двигатель
|
47
|
Итоги
- Механические устройства, с помощью которых можно изменять направление и модуль силы, называют простыми механизмами.
- Неподвижный блок не даёт выигрыша или проигрыша ни в силе, ни в расстоянии.
- Подвижный блок даёт выигрыш в силе в 2 раза и проигрыш в расстоянии 2 раза.
- Золотое правило механики: во сколько раз мы выигрываем в силе, во столько же раз проигрываем в расстоянии и наоборот.
- Отношение полезной работы к затраченной работе называют коэффициентом полезного действия (КПД) механизма: .
Упражнение 1
1. При подъёме груза массой 100 кг на высоту 3 м с помощью механизма была затрачена работа 3 200 Дж. Чему равно КПД этого механизма?
Контрольные вопросы
1. Что такое простые механизмы?
2. Какие виды блоков вы знаете?
3. В чём состоит «золотое правило механики»?
4. Продемонстрируйте справедливость золотого правила механики на примере работы подвижного и неподвижного блоков.
5. Что такое КПД механизма?
6. Может ли КПД быть равным 2?
7. Что означает, что КПД равно 80 %?
Упражнение 1
1. КПД = 0,94 или 94 %.



