- Окружность и круг
- Длина окружности. Площадь круга
- Знать понятия: круг, окружность, диаметр, радиус, хорда, центр окружности, формулы для нахождения длины окружности и площади круга, как чертить окружность с помощью циркуля, строить треугольник с заданными длинами сторон с помощью циркуля и линейки.
- Уметь решать задачи на нахождение длины окружности и площади круга, проводить радиусы, хорды и диаметры окружности, строить треугольник с заданными длинами сторон с помощью циркуля и линейки, чертить окружность с помощью циркуля.
- Какие геометрические фигуры вы знаете?
- Существует ли плоская фигура, не имеющая углов?
Окружность и круг
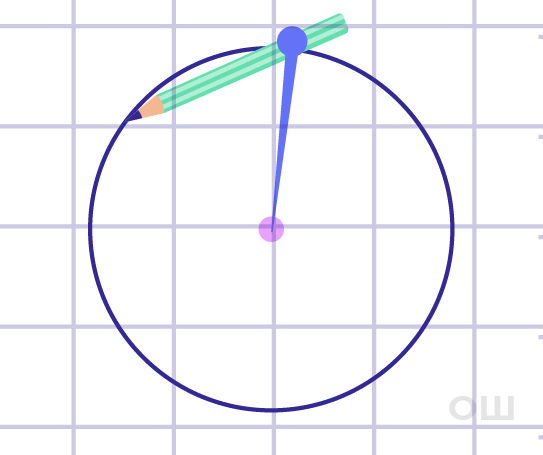 Рис. 1. Построение окружности с помощью циркуля
Рис. 1. Построение окружности с помощью циркуля
Круглые тела еще в древности заинтересовали человека. В Древнем Египте для постройки знаменитых египетских пирамид никаких технических сооружений еще не было. Даже шлифовать огромные каменные глыбы приходилось вручную, а перемещали их с помощью бревен круглой формы. Заметили, что перекатка проще, если взять кусок дерева с почти одинаковой толщиной в начале и в конце. Так люди познакомились с одним из важнейших тел — цилиндром. Скалками цилиндрической формы пользовались и женщины, раскатывая белье после стирки. Перевозить грузы на катках было довольно тяжело, потому что сами древесные стволы весили много. Чтобы облегчить работу, стали вырезать из стволов тонкие круглые пластинки, которые катились уже легче и с их помощью перетаскивали грузы. Так появилось первое колесо.
Для построения окружности используют циркуль (рис. 1). Точка, в которую ставится игла циркуля, называется центром окружности. Другая ножка циркуля при вращении опишет окружность.
 Рис. 2. Окружность
Рис. 2. Окружность
Окружность — множество точек плоскости, расположенных на одинаковом расстоянии от данной точки (центр окружности).
На рис. 2 О — центр окружности.
Радиус — отрезок, соединяющий центр окружности с любой ее точкой. Обозначается r.
OC, OA, OM, OK — радиусы (рис. 2).
Хорда — отрезок, соединяющий любые две точки окружности.
AM, CK — хорды.
Диаметр — хорда, проходящая через центр окружности. Обозначается d.
CK — диаметр.
Все радиусы окружности равны.
Все диаметры окружности равны.
Точки М и С, лежащие на окружности (рис. 2) делят ее на две части. Части окружности, заключенные между точками М и С, называется дугами.
Взаимосвязь радиуса и диаметра
Заметим, что диаметр CK на рис. 2 состоит из двух отрезков OK и OC, которые в свою очередь являются радиусами этой окружности. Значит, длина диаметра окружности равна длине двух радиусов, а длина радиуса равна половине длины диаметра окружности.
где r — радиус окружности, d — диаметр окружности.
 Рис. 3. Круг
Рис. 3. Круг
Окружность представляет собой замкнутую линию. Она ограничивает часть плоскости. Эту часть плоскости вместе с окружностью называют кругом.
Круг, как и окружность, имеет центр, радиус, в нем можно провести диаметр и другие хорды.
На рис. 3 построен круг и проведены радиусы. Часть круга, ограниченная двумя радиусами и дугой, заключенной между ними, называется сектором. Если мы говорим о части круга, ограниченной хордой и «стянутой» ей дугой, то это сегмент круга.
 Рис.4. Полукруг
Рис.4. Полукруг
Точки, удаленные от центра круга на расстояние, меньшее радиуса круга или равное ему, принадлежат кругу.
Точки A и B на рис. 3 принадлежат кругу, точка С не принадлежит кругу.
На рис. 4 диаметр CF делит круг на две равные части, каждую из которых называют полукругом.
Пример 1
С помощью циркуля и линейки постройте треугольник ABC с со сторонами AB = 5 см, AC = 4 см, BC = 3 см.
Решение
 Рис. 5. Построение треугольника ABC с помощью циркуля и линейки
Рис. 5. Построение треугольника ABC с помощью циркуля и линейки
Строим с помощью линейки отрезок AB, равный 5 см. Вершина С должна быть удалена от точки А на 4 см, а от точки В на 3 см, т.е. она должна быть точкой пересечения окружностей радиуса 3 см и 4 см. Построим окружности с центром в точке А и радиусом 4 см и с центром в точке B и радиусом 3 см.
Окружности пересекаются в двух точках. Выберем любую из них и обозначим как точку С. Проведем отрезки AC и BC.
Треугольник ABC — искомый.
 Рис. 6. Длина окружности
Рис. 6. Длина окружности
Длина окружности. Площадь круга
Представьте, что окружность обернута нитью. Если разрезать эту нить в некоторой точке и размотать ее, то длина нити будет равна длине окружности. Обычно длину окружности обозначают .
Заметим, что чем больше диаметр у окружности, тем больше длина окружности. Значит диаметр окружности и ее длина — прямо пропорциональные величины, поэтому для всех окружностей отношение этих величин одинаковое. Его обозначают греческой буквой (читается «пи»).
.
Отсюда
.
Еще в древности установили, что . Если перевести эту дробь в периодическую и округлить до сотых, получим .
Так как диаметр вдвое больше радиуса, то можно выразить формулу длины окружности как через диаметр, так и через радиус.
Площадь круга тоже зависит от его радиуса. Ниже приведем формулы для нахождения длины окружности и площади круга.
Формула длины окружности и площади круга
где l — длина окружности, S — площадь круга, d — диаметр, r — радиус.
Упражнения
 Рис. 7. Чертеж к упражнению 1
Рис. 7. Чертеж к упражнению 1
1. Укажите центр, радиус, хорду и диаметр окружности, изображённой на рис. 7.
2. Вычислите длину окружности, диаметр которой равен 4,7 см ( = 3,14).
3. Вычислите длину окружности, радиус которой равен 1,5 см ( = 3,14).
4. Найдите площадь круга, радиус которого равен 4 см ( = 3,14).
Контрольные вопросы
1. Что такое окружность?
2. Чем отличается диаметр от хорды?
3. Что такое радиус?
4. В чем отличие круга от окружности?
5. Как найти площадь круга?
6. Как найти длину окружности?
7. Назовите значение числа
1. A — центр; AW, AN, AR — радиусы; WR, DS — хорды; WR — диаметр.
2. 14,758 см
3. 9,42 см
4. 50,24 см2.
- Окружность и круг
- Длина окружности. Площадь круга
- Знать понятия: круг, окружность, диаметр, радиус, хорда, центр окружности, формулы для нахождения длины окружности и площади круга, как чертить окружность с помощью циркуля, строить треугольник с заданными длинами сторон с помощью циркуля и линейки.
- Уметь решать задачи на нахождение длины окружности и площади круга, проводить радиусы, хорды и диаметры окружности, строить треугольник с заданными длинами сторон с помощью циркуля и линейки, чертить окружность с помощью циркуля.
- Какие геометрические фигуры вы знаете?
- Существует ли плоская фигура, не имеющая углов?
Окружность и круг
 Рис. 1. Построение окружности с помощью циркуля
Рис. 1. Построение окружности с помощью циркуля
Круглые тела еще в древности заинтересовали человека. В Древнем Египте для постройки знаменитых египетских пирамид никаких технических сооружений еще не было. Даже шлифовать огромные каменные глыбы приходилось вручную, а перемещали их с помощью бревен круглой формы. Заметили, что перекатка проще, если взять кусок дерева с почти одинаковой толщиной в начале и в конце. Так люди познакомились с одним из важнейших тел — цилиндром. Скалками цилиндрической формы пользовались и женщины, раскатывая белье после стирки. Перевозить грузы на катках было довольно тяжело, потому что сами древесные стволы весили много. Чтобы облегчить работу, стали вырезать из стволов тонкие круглые пластинки, которые катились уже легче и с их помощью перетаскивали грузы. Так появилось первое колесо.
Для построения окружности используют циркуль (рис. 1). Точка, в которую ставится игла циркуля, называется центром окружности. Другая ножка циркуля при вращении опишет окружность.
 Рис. 2. Окружность
Рис. 2. Окружность
Окружность — множество точек плоскости, расположенных на одинаковом расстоянии от данной точки (центр окружности).
На рис. 2 О — центр окружности.
Радиус — отрезок, соединяющий центр окружности с любой ее точкой. Обозначается r.
OC, OA, OM, OK — радиусы (рис. 2).
Хорда — отрезок, соединяющий любые две точки окружности.
AM, CK — хорды.
Диаметр — хорда, проходящая через центр окружности. Обозначается d.
CK — диаметр.
Все радиусы окружности равны.
Все диаметры окружности равны.
Точки М и С, лежащие на окружности (рис. 2) делят ее на две части. Части окружности, заключенные между точками М и С, называется дугами.
Взаимосвязь радиуса и диаметра
Заметим, что диаметр CK на рис. 2 состоит из двух отрезков OK и OC, которые в свою очередь являются радиусами этой окружности. Значит, длина диаметра окружности равна длине двух радиусов, а длина радиуса равна половине длины диаметра окружности.
где r — радиус окружности, d — диаметр окружности.
 Рис. 3. Круг
Рис. 3. Круг
Окружность представляет собой замкнутую линию. Она ограничивает часть плоскости. Эту часть плоскости вместе с окружностью называют кругом.
Круг, как и окружность, имеет центр, радиус, в нем можно провести диаметр и другие хорды.
На рис. 3 построен круг и проведены радиусы. Часть круга, ограниченная двумя радиусами и дугой, заключенной между ними, называется сектором. Если мы говорим о части круга, ограниченной хордой и «стянутой» ей дугой, то это сегмент круга.
 Рис.4. Полукруг
Рис.4. Полукруг
Точки, удаленные от центра круга на расстояние, меньшее радиуса круга или равное ему, принадлежат кругу.
Точки A и B на рис. 3 принадлежат кругу, точка С не принадлежит кругу.
На рис. 4 диаметр CF делит круг на две равные части, каждую из которых называют полукругом.
Пример 1
С помощью циркуля и линейки постройте треугольник ABC с со сторонами AB = 5 см, AC = 4 см, BC = 3 см.
Решение
 Рис. 5. Построение треугольника ABC с помощью циркуля и линейки
Рис. 5. Построение треугольника ABC с помощью циркуля и линейки
Строим с помощью линейки отрезок AB, равный 5 см. Вершина С должна быть удалена от точки А на 4 см, а от точки В на 3 см, т.е. она должна быть точкой пересечения окружностей радиуса 3 см и 4 см. Построим окружности с центром в точке А и радиусом 4 см и с центром в точке B и радиусом 3 см.
Окружности пересекаются в двух точках. Выберем любую из них и обозначим как точку С. Проведем отрезки AC и BC.
Треугольник ABC — искомый.
 Рис. 6. Длина окружности
Рис. 6. Длина окружности
Длина окружности. Площадь круга
Представьте, что окружность обернута нитью. Если разрезать эту нить в некоторой точке и размотать ее, то длина нити будет равна длине окружности. Обычно длину окружности обозначают .
Заметим, что чем больше диаметр у окружности, тем больше длина окружности. Значит диаметр окружности и ее длина — прямо пропорциональные величины, поэтому для всех окружностей отношение этих величин одинаковое. Его обозначают греческой буквой (читается «пи»).
.
Отсюда
.
Еще в древности установили, что . Если перевести эту дробь в периодическую и округлить до сотых, получим .
Так как диаметр вдвое больше радиуса, то можно выразить формулу длины окружности как через диаметр, так и через радиус.
Площадь круга тоже зависит от его радиуса. Ниже приведем формулы для нахождения длины окружности и площади круга.
Формула длины окружности и площади круга
где l — длина окружности, S — площадь круга, d — диаметр, r — радиус.
Упражнения
 Рис. 7. Чертеж к упражнению 1
Рис. 7. Чертеж к упражнению 1
1. Укажите центр, радиус, хорду и диаметр окружности, изображённой на рис. 7.
2. Вычислите длину окружности, диаметр которой равен 4,7 см ( = 3,14).
3. Вычислите длину окружности, радиус которой равен 1,5 см ( = 3,14).
4. Найдите площадь круга, радиус которого равен 4 см ( = 3,14).
Контрольные вопросы
1. Что такое окружность?
2. Чем отличается диаметр от хорды?
3. Что такое радиус?
4. В чем отличие круга от окружности?
5. Как найти площадь круга?
6. Как найти длину окружности?
7. Назовите значение числа
1. A — центр; AW, AN, AR — радиусы; WR, DS — хорды; WR — диаметр.
2. 14,758 см
3. 9,42 см
4. 50,24 см2.



