Симметрия в пространстве. Понятие правильного многогранника. Элементы симметрии правильных многогранников

Правильные многогранники

План урока

Симметрия в пространстве;
Понятие правильного многогранника;
Элементы симметрии правильных многогранников.

Цели урока

Знать, какие точки называются симметричными относительно точки, симметричными относительно прямой и симметричными относительно плоскости;
Знать и уметь приводить примеры симметрии в природе, архитектуре, технике и быту;
Знать, какой многогранник называется правильным;
Знать названия правильных многогранников и из каких фигур состоят их поверхности;
Уметь находить элементы симметрии правильных многогранников.

Разминка

Какую фигуру на плоскости называют правильным многоугольником?
Чему равна сумма углов правильного $n$ -угольника?
Какую геометрическую фигуру называют тетраэдром?
Какую геометрическую фигуру называют кубом?

Симметрия в пространстве

В курсе планиметрии вы уже знакомились с понятием симметрии и рассматривали фигуры, симметричные относительно точки и относительно прямой.

В пространстве кроме симметрии относительно точки и прямой, рассматривают ещё и симметрию относительно плоскости.

Сформулируем определение каждого вида симметрии.

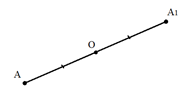Рис. 1. Симметрия относительно точки

Точки $A$ и $A_{1}$ называются симметричными относительно точки $O$ , если $O$ – середина отрезка $A A_{1}$ (рис. 1).

Точка $O$ при этом называется центром симметрии и считается симметричной самой себе.

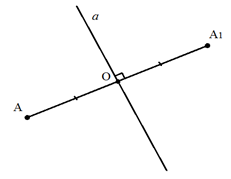Рис. 2. Симметрия относительно прямой

Точки $A$ и $A_{1}$ называются симметричными относительно прямой $a$ , если прямая $a$ проходит через середину отрезка $A A_{1}$ и перпендикулярна к этому отрезку (рис. 2).

Прямая $a$ при этом называется осью симметрии, а любая точка этой прямой считается симметричной самой себе.

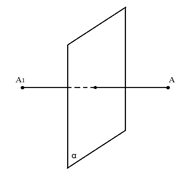Рис. 3. Симметрия относительно плоскости

Точки $A$ и $A_{1}$ называются симметричными относительно плоскости $α$ , если плоскость $α$ проходит через середину отрезка $A A_{1}$ и перпендикулярна к этому отрезку (рис. 3).

Плоскость $α$ при этом называется плоскостью симметрии, а любая точка этой плоскости считается симметричной самой себе.

Сформулируем теперь определение понятий центра, оси и плоскости симметрии фигуры.

Точка (прямая, плоскость) называется центром (осью, плоскостью) симметрии фигуры, если каждая точка фигуры симметрична относительно неё некоторой точке той же фигуры.

Про фигуру в таком случае говорят, что она имеет центр (ось,
плоскость) симметрии.

Если фигура имеет центр (ось, плоскость) симметрии, то говорят, что она обладает центральной (осевой, зеркальной) симметрией.

Рис. 4. а) центр; б) ось; в) плоскость - симметрии

На рисунке 4 изображён прямоугольный параллелепипед и его центр $O$ , ось $a$ и плоскость $α$ симметрии.

Фигура может иметь несколько и даже бесконечное множество центров (осей, плоскостей) симметрии, а может и не иметь центра (оси, плоскости) симметрии.

Центры, оси и плоскости симметрии геометрической фигуры называются элементами симметрии данной фигуры.

Рис. 5. Примеры симметрии в нашей жизни

В окружающем мире часто можно встретить предметы, обладающие тем или иным элементом симметрии. Симметричность воспринимается как признак красоты и совершенства. В быту и технике чаще именно симметричные предметы и устройства бывают наиболее удобными в использовании.

На рисунке 5 показаны примеры симметрии в окружающем мире.

Понятие правильного многогранника

Выпуклый многогранник называется правильным, если все его

грани – равные правильные многоугольники и в каждой его вершине сходится одно и то же число рёбер.

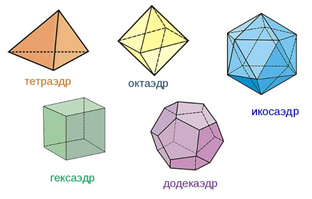Рис. 6. Правильные многогранники

Существует пять типов правильных многогранников: правильный тетраэдр, куб (гексаэдр), октаэдр, додекаэдр, икосаэдр (рис. 6).

У правильного тетраэдра грани – правильные треугольники; в каждой вершине сходятся три ребра. Правильный тетраэдр представляет собой треугольную пирамиду, у которой все рёбра равны.

У куба все грани квадраты; в каждой вершине сходятся три ребра. Куб представляет собой прямоугольный параллелепипед с равными рёбрами.

У октаэдра грани – правильные треугольники, но в отличие от тетраэдра в каждой его вершине сходятся четыре ребра.

У додекаэдра грани – правильные пятиугольники. В каждой вершине сходятся три ребра.

У икосаэдра грани – правильные треугольники, но в отличие от тетраэдра и октаэдра в каждой вершине сходятся пять рёбер.

Математиками доказано, что не существует правильного многогранника, гранями которого являются правильные
n-угольники при $n \geq 6$ .

Пример 1

Найдите двугранные углы правильного тетраэдра.

Решение

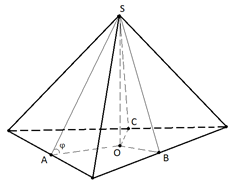Рис. 7. К примеру 1

Проведём из вершины $S$ тетраэдра высоты $S A$ , $S B$ , $S C$ его граней, сходящихся в этой вершине, и высоту $S O$ тетраэдра (рис. 7). Если ребро тетраэдра обозначить $a$ , то высоты граней будут равны $\frac{a \sqrt{3}}{2}$ .

Из равенства высот $S A$ , $S B$ , $S C$ следует равенство отрезков $O A$ , $O B$ , $O C$ . А они перпендикулярны сторонам треугольника в основании тетраэдра (по теореме о трёх перпендикулярах). Отсюда следует, что точка $O$ является центром окружности, вписанной в основание тетраэдра. Следовательно, отрезки $O A$ , $O B$ и $O C$ равны $\frac{a \sqrt{3}}{6}$ . Обозначим буквой $φ$ двугранный угол при ребре, содержащей точку $A$ . Тогда

$\cos φ = \frac{O A}{A S} = \frac{a \sqrt{3}}{6} : \frac{a \sqrt{3}}{2} = \frac{1}{3}$

$φ = a r c \cos \frac{1}{3}$ .

Двугранные углы при остальных рёбрах тетраэдра такие же по величине.

Ответ: $a r c \cos \frac{1}{3}$ .

Элементы симметрии правильных многогранников

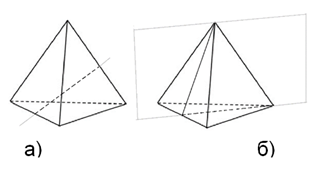Рис. 8.

Тетраэдр имеет три оси симметрии, которые проходят через середины двух противоположных ребер (рис. 8 а).

Тетраэдр имеет 6 плоскостей симметрии, каждая из которых проходит через ребро тетраэдра перпендикулярно скрещивающемуся с ним ребру (рис. 8 б).

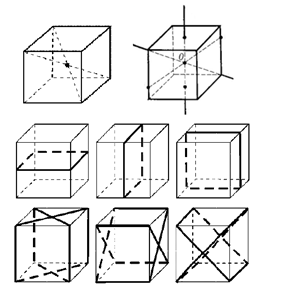Рис. 9.

Куб (рис. 9) имеет один центр симметрии. Центром симметрии куба является точка пересечения его диагоналей.

Ось симметрии куба может проходить либо через середины параллельных ребер, не принадлежащих одной грани, либо через точки пересечения диагоналей противоположных граней.

Через центр симметрии проходят девять осей симметрии.

Плоскостей симметрии у куба также девять и проходят они либо через противоположные ребра, либо через середины противоположных ребер.

Правильный октаэдр, правильный икосаэдр и правильный додекаэдр имеют центр симметрии и несколько осей и плоскостей симметрии.

Упражнение 1

1. Сколько центров симметрии имеет:

а) отрезок; б) треугольник; в) параллелепипед

2. Сколько осей симметрии имеет:

а) отрезок; б) куб

3. Сколько плоскостей симметрии имеет правильная четырёхугольная призма, отличная от куба?

Контрольные вопросы

Объясните, что такое центр симметрии, ось симметрии и плоскость симметрии.
Сформулируйте определение правильного многогранника.
Какие многоугольники могут быть гранями правильного многогранника?

Ответы

Упражнение 1

а) один; б) не имеет; в) один
а) бесконечное множество; б) девять
пять

Конспект урока: Симметрия в пространстве. Понятие правильного многогранника. Элементы симметрии правильных многогранников

Общие сведения из стереометрии

Симметрия в пространстве

Понятие правильного многогранника

Элементы симметрии правильных многогранников