- Абсолютно твёрдое тело. Поступательное и вращательное движение твёрдого тела
- знать понятия: твёрдое тело, поступательное и вращательное движение
- уметь приводить примеры поступательного и вращательного движения; определять скорость точки вращающегося тела
- Что такое точечное тело?
- Какое тело называют абсолютно твёрдым?
- Какое движение называют поступательным?
Абсолютно твёрдое тело. Поступательное и вращательное движение твёрдого тела
В предыдущих параграфах при выводе законов движения мы заменяли реальные объекты на их модели — точечные тела. Понятно, что в реальности тела имеют конечные размеры, помимо этого, части тела могут подчиняться разным законам движения. Реальное тело можно представить как совокупность бесконечно большого количества точек, движение такого тела можно считать полностью описанным лишь при условии, что известны законы движения каждой его точки. Понятно, что описать движение каждой точки тела невозможно. Рассмотрение движения реальных тел начинают с двух простых видов движения: поступательного и вращательного, но прежде чем с ними познакомиться, необходимо ввести понятие твёрдого тела.
Реальные тела зачастую деформируются в процессе движения, следовательно, изменяются расстояния между двумя точками данного тела. Если деформации много меньше размеров самих тел, деформациями можно пренебречь. В этом случае тело называют твёрдым (или абсолютно твёрдым).
Тело называется твёрдым, если расстояние между любыми двумя точками данного тела не изменяется с течением времени.
Иначе говоря, у твёрдого тела не меняется взаимное расположение его частей. Понятно, что твёрдое тело — это лишь модель реального объекта: в природе не существует твёрдых тел.
 Рис. 1. Поступательное движение кабины колеса обозрения
Рис. 1. Поступательное движение кабины колеса обозрения
Поступательное движение означает, что все точки твёрдого тела имеют одинаковые вектора скорости в любой момент времени. То есть любая точка тела движется с одинаковой по модулю скоростью и в одном и том же направлении.
Например, кабина колеса обозрения движется поступательно: несмотря на то что тело движется по окружности, все точки, принадлежащие ему, движутся в одном направлении и с одинаковыми скоростями (рис. 1). В данном случае для описания характера движения кабины достаточно описать движение одной её точки, поэтому кабину колеса обозрения можно принять за точечное тело.
 Рис. 2. АВ//А’B’//A’’B’’
Рис. 2. АВ//А’B’//A’’B’’
Понятно, что если все точки рассматриваемого тела имеют одинаковые направления и модули скорости, то прямая, проведённая через любые две точки этого тела, при движении данного тела в любой момент времени будет оставаться параллельной своему исходному положению (рис. 2).
Поступательным называют такое движение твёрдого тела, при котором прямая, проведённая через любые две точки данного тела, в процессе движения остаётся параллельной своему начальному положению.
Если задано начальное положение твёрдого тела и закон движения одной его точки, то можно определить положение любой другой точки тела в любой момент времени.
Например, пусть известны начальное положение твёрдого тела неправильной формы и закон движения точки A, принадлежащей данному телу (рис. 2). Тогда, используя закон движения, можно найти положение A’ точки А в любой последующий момент времени. Чтобы определить положение B’ точки B в тот же момент времени, необходимо построить прямую A’B’, параллельную прямой АВ и проходящую через точку A’. Если отложить на полученной прямой отрезок A’B’, равный отрезку АВ, то мы найдём положение B’ точки B.
Вращательным называют такое движение твёрдого тела, при котором все его точки движутся по окружностям, центры которых лежат на одной неподвижной прямой. Эту прямую называют осью вращения.
 Рис. 3 Вращение Земли
Рис. 3 Вращение Земли
Самый простой пример вращательного движения — вращение Земли вокруг своей оси (рис. 3).
Угловые скорости всех точек вращающегося тела равны. Скорость точки вращающегося тела называется угловой скоростью вращения твёрдого тела.
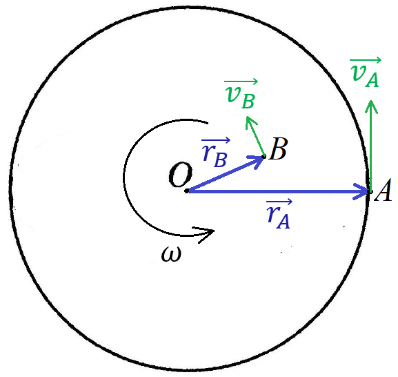
На рисунке 4 показан диск, вращающийся с угловой скоростью . Скорость вращения каждой точки вращающегося твёрдого тела направлена по касательной к окружности, по которой движется данная точка. Понятно, что в этом случае вектор скорости точки будет перпендикулярен радиус-вектору, проведённому в данную точку: и .
 A> 𝑣B" loading="lazy" />
Рис. 4. 𝑣A> 𝑣B
A> 𝑣B" loading="lazy" />
Рис. 4. 𝑣A> 𝑣B
Модуль скорости точки вращающегося тела определяется по формуле , следовательно, модуль скорости зависит от угловой скорости вращения и расстояния от оси вращения до данной точки R.
Так, для модуль скорости вращения точки A равен , а модуль скорости вращения точки B равен .
Так как ОА > OB, скорость вращения точки A больше скорости вращения точки B:
.
Чем больше расстояние между осью вращения и рассматриваемой точкой, тем больше модуль скорости её вращения.
Итоги
- Поступательным называют такое движение твёрдого тела, при котором прямая, проведённая через любые две точки данного тела, в процессе движения остаётся параллельной своему начальному положению.
- Вращательным называют такое движение твёрдого тела, при котором все его точки движутся по окружностям, центры которых лежат на одной неподвижной прямой. Эту прямую называют осью вращения.
- Чем больше расстояние между осью вращения и рассматриваемой точкой, тем больше модуль скорости её вращения.
Контрольные вопросы
1. Какое движение называется поступательным?
2. Какое движение называется вращательным?
3. Как рассчитывается модуль скорости точки вращающегося тела?
- Абсолютно твёрдое тело. Поступательное и вращательное движение твёрдого тела
- знать понятия: твёрдое тело, поступательное и вращательное движение
- уметь приводить примеры поступательного и вращательного движения; определять скорость точки вращающегося тела
- Что такое точечное тело?
- Какое тело называют абсолютно твёрдым?
- Какое движение называют поступательным?
Абсолютно твёрдое тело. Поступательное и вращательное движение твёрдого тела
В предыдущих параграфах при выводе законов движения мы заменяли реальные объекты на их модели — точечные тела. Понятно, что в реальности тела имеют конечные размеры, помимо этого, части тела могут подчиняться разным законам движения. Реальное тело можно представить как совокупность бесконечно большого количества точек, движение такого тела можно считать полностью описанным лишь при условии, что известны законы движения каждой его точки. Понятно, что описать движение каждой точки тела невозможно. Рассмотрение движения реальных тел начинают с двух простых видов движения: поступательного и вращательного, но прежде чем с ними познакомиться, необходимо ввести понятие твёрдого тела.
Реальные тела зачастую деформируются в процессе движения, следовательно, изменяются расстояния между двумя точками данного тела. Если деформации много меньше размеров самих тел, деформациями можно пренебречь. В этом случае тело называют твёрдым (или абсолютно твёрдым).
Тело называется твёрдым, если расстояние между любыми двумя точками данного тела не изменяется с течением времени.
Иначе говоря, у твёрдого тела не меняется взаимное расположение его частей. Понятно, что твёрдое тело — это лишь модель реального объекта: в природе не существует твёрдых тел.
 Рис. 1. Поступательное движение кабины колеса обозрения
Рис. 1. Поступательное движение кабины колеса обозрения
Поступательное движение означает, что все точки твёрдого тела имеют одинаковые вектора скорости в любой момент времени. То есть любая точка тела движется с одинаковой по модулю скоростью и в одном и том же направлении.
Например, кабина колеса обозрения движется поступательно: несмотря на то что тело движется по окружности, все точки, принадлежащие ему, движутся в одном направлении и с одинаковыми скоростями (рис. 1). В данном случае для описания характера движения кабины достаточно описать движение одной её точки, поэтому кабину колеса обозрения можно принять за точечное тело.
 Рис. 2. АВ//А’B’//A’’B’’
Рис. 2. АВ//А’B’//A’’B’’
Понятно, что если все точки рассматриваемого тела имеют одинаковые направления и модули скорости, то прямая, проведённая через любые две точки этого тела, при движении данного тела в любой момент времени будет оставаться параллельной своему исходному положению (рис. 2).
Поступательным называют такое движение твёрдого тела, при котором прямая, проведённая через любые две точки данного тела, в процессе движения остаётся параллельной своему начальному положению.
Если задано начальное положение твёрдого тела и закон движения одной его точки, то можно определить положение любой другой точки тела в любой момент времени.
Например, пусть известны начальное положение твёрдого тела неправильной формы и закон движения точки A, принадлежащей данному телу (рис. 2). Тогда, используя закон движения, можно найти положение A’ точки А в любой последующий момент времени. Чтобы определить положение B’ точки B в тот же момент времени, необходимо построить прямую A’B’, параллельную прямой АВ и проходящую через точку A’. Если отложить на полученной прямой отрезок A’B’, равный отрезку АВ, то мы найдём положение B’ точки B.
Вращательным называют такое движение твёрдого тела, при котором все его точки движутся по окружностям, центры которых лежат на одной неподвижной прямой. Эту прямую называют осью вращения.
 Рис. 3 Вращение Земли
Рис. 3 Вращение Земли
Самый простой пример вращательного движения — вращение Земли вокруг своей оси (рис. 3).
Угловые скорости всех точек вращающегося тела равны. Скорость точки вращающегося тела называется угловой скоростью вращения твёрдого тела.
На рисунке 4 показан диск, вращающийся с угловой скоростью . Скорость вращения каждой точки вращающегося твёрдого тела направлена по касательной к окружности, по которой движется данная точка. Понятно, что в этом случае вектор скорости точки будет перпендикулярен радиус-вектору, проведённому в данную точку: и .
 A> 𝑣B" loading="lazy" />
Рис. 4. 𝑣A> 𝑣B
A> 𝑣B" loading="lazy" />
Рис. 4. 𝑣A> 𝑣B
Модуль скорости точки вращающегося тела определяется по формуле , следовательно, модуль скорости зависит от угловой скорости вращения и расстояния от оси вращения до данной точки R.
Так, для модуль скорости вращения точки A равен , а модуль скорости вращения точки B равен .
Так как ОА > OB, скорость вращения точки A больше скорости вращения точки B:
.
Чем больше расстояние между осью вращения и рассматриваемой точкой, тем больше модуль скорости её вращения.
Итоги
- Поступательным называют такое движение твёрдого тела, при котором прямая, проведённая через любые две точки данного тела, в процессе движения остаётся параллельной своему начальному положению.
- Вращательным называют такое движение твёрдого тела, при котором все его точки движутся по окружностям, центры которых лежат на одной неподвижной прямой. Эту прямую называют осью вращения.
- Чем больше расстояние между осью вращения и рассматриваемой точкой, тем больше модуль скорости её вращения.
Контрольные вопросы
1. Какое движение называется поступательным?
2. Какое движение называется вращательным?
3. Как рассчитывается модуль скорости точки вращающегося тела?



