- Корень -й степени;
- Нахождение значения корня -й степени;
- Арифметический корень -й степени.
- Знать определение корня -й степени;
- Знать определение арифметического корня -й степени;
- Уметь находить корень -й степени из числа.
- Как прочитать эту запись: ?
- Чему равны корни уравнения ?
- Имеет ли решение уравнение ?
Корень -й степени
Решим уравнения и . Первое уравнение ни у кого из вас не должно вызвать сложности:
, , .
Второе уравнение выглядит немного сложнее, так как нет такого целого числа, которое при возведении в квадрат дало бы 11. Для записи решения таких уравнений в математике есть специальный символ: . Тогда можем легко записать решение для второго уравнения:
, , .
Напомним, что числа, которые записываются с помощью корня квадратного () называются иррациональными, а квадратным корнем из числа называется такое число, квадрат которого равен :
, если .
Аналогично определяется корень любой натуральной степени .
Корнем -й степени из числа называется такое число, -я степень которого равна .
Нахождение значения корня -й степени
Рассмотрим степенную функцию с нечётным показателем (рис.1). Для любого числа существует единственное значение , -я степень которого равна Это значение является корнем -й степени из числа . Для записи корня нечётной степени из числа используют обозначение (читают: «корень -й степени из »).
 n, n-нечётное" loading="lazy" />
Рис. 1. Функция y=xn, n-нечётное
n, n-нечётное" loading="lazy" />
Рис. 1. Функция y=xn, n-нечётное
Число называют показателем корня, выражение, стоящее под знаком корня, - подкоренным выражением.
Пример 1
Вычислить и .
Решение
Из определения корня следует, что , так как .
Аналогично, из определения корня следует, что , так как
Ответ: ; .
Упражнение 1
- 2. 3.
 n, n-чётное" loading="lazy" />
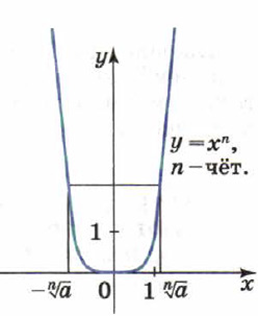
Рис. 2. Функция y=xn, n-чётное
n, n-чётное" loading="lazy" />
Рис. 2. Функция y=xn, n-чётное
Рассмотрим теперь степенную функцию с чётным показателем (рис.2). При любом существуют два противоположных значения , -я степень которых равна . При такое число одно (число 0), при таких чисел нет. Другими словами, если чётное число и , то существует два корня -й степени из . Эти корни являются противоположными числами. Если , то корень -й степени из равен нулю.
Если и - чётное число, то корня -й степени из не существует.
В случае чётного знаком обозначают неотрицательный корень -й степени из . Отрицательный корень -й степени из (при ) записывается так:
Выражение при чётном и не имеет смысла.
Если , то показатель не пишется ().
Пример 2
Вычислить .
Решение
Запись означает неотрицательный корень четвёртой степени из 16.
Имеем , так как - неотрицательное число и .
Ответ: .
Упражнение 2
Вычислить:
- 2. 3.
Арифметический корень -й степени
Итак, если - нечётное число, то выражение имеет смысл при любом ; если - чётное число, то выражение имеет смысл лишь при любом .
При всех значениях , при которых выражение имеет смысл, верно равенство .
Выражение при имеет смысл как при чётном, так и при нечётном , и значение этого выражения является неотрицательным числом. Его называют арифметическим корнем -й степени из .
Арифметическим корнем -й степени из неотрицательного числа называется неотрицательное число, -я степень которого равна .
Корень нечётной степени из отрицательного числа можно выразить через арифметический корень.
Например, , так как и .
При любом нечётном и положительном верно равенство .
При нахождении корня -й степени из положительного числа используют представление выражения , где , в виде степени числа с дробным показателем.
Если и - натуральное число, большее 1, считают, что
.
Упражнение 3
1. Найдите значение выражения:
а) б) в)
2. Представьте корень -й степени в виде числа в дробной степени:
а) б) в)
Контрольные вопросы:
1. Корень какой степени можно извлекать из отрицательных чисел?
2. Чем арифметический корень -й степени отличается от корня -й степени?
3. Что будет, если корень -й степени возвести в степень ?
Упражнение 1
1. 6. 2. -0,3. 3. 1,5
Упражнение 2
1. 16. 2. -0,5. 3. 0,8
Упражнение 3
1. а) 320; б) -224; в) 4802.
2. а) ; б) ; в) .

