Все уроки по всем предметам школьной программы ФГОС

Компланарные векторы

План урока

Компланарные векторы
Правило параллелепипеда
Разложение вектора по трем некомпланарным векторам

Цели урока

Знать определение компланарных векторов
Знать и уметь доказывать признак компланарности трёх векторов
Знать и уметь применять правило параллелепипеда сложения трёх некомпланарных векторов
Знать и уметь доказывать теорему о разложении вектора по трём некомпланарным векторам
Уметь находить разложение вектора по трём данным некомпланарным векторам

Разминка

Какие векторы называются коллинеарными?
Сколько плоскостей проходит через три точки, не лежащие на одной прямой?
Две стороны треугольника параллельны плоскости $α$ . Параллельна ли третья сторона плоскости $α$ ?

Компланарные векторы

Определение 1

Компланарные векторы — это векторы, которые параллельны одной плоскости или лежат в одной плоскости (рис. 1).

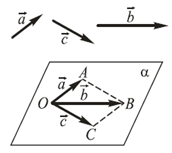Рис. 1. Компланарные вектора

Можно также сказать, что векторы называются компланарными, если при откладывании их от одной точки они будут лежать в одной плоскости (другими словами, имеются равные им векторы, лежащие в одной плоскости).

Из определения следует, что любые два векторы компланарны, а три произвольных вектора могут быть как компланарными, так и не компланарными.

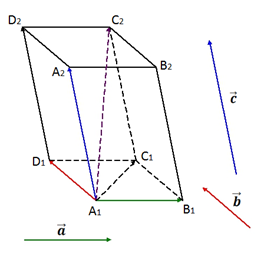Рис. 2.

На рисунке 2 изображён параллелепипед.

Векторы $\vec{D_{1} D_{2}}$ , $\vec{A_{1} C_{2}}$ , $\vec{A_{1} C_{1}}$ компланарны, так как если отложить от точки $A_{1}$ вектор, равный $\vec{D_{1} D_{2}}$ , то получится $\vec{A_{1} A_{2}}$ , а векторы $\vec{A_{1} A_{2}}$ ,
$\vec{A_{1} C_{2}}$ , $\vec{A_{1} C_{1}}$ лежат в одной плоскости $A_{2} A_{1} C_{1}$ .

Векторы $\vec{A_{1} D_{1}}$ , $\vec{A_{1} B_{1}}$ , $\vec{A_{1} A_{2}}$ не компланарны, так вектор $\vec{A_{1} A_{2}}$ не лежит в плоскости $D_{1} A_{1} B_{1}$ .

Теорема 1 (признак компланарности трёх векторов)

Если вектор $\vec{c}$ можно разложить по векторам $\vec{a}$ и $\vec{b}$ , т.е. представить в виде $\vec{с} = x \vec{a} + y \vec{b}$ , где $x$ и $y$ – некоторые числа, то векторы $\vec{a}$ , $\vec{b}$ и $\vec{c}$ компланарны.

Доказательство

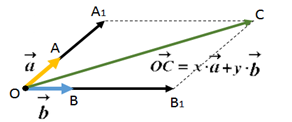Рис. 3. К теореме 1

Если векторы $\vec{a}$ и $\vec{b}$ коллинеарны, то компланарность векторов $\vec{a}$ , $\vec{b}$ и $\vec{c}$ очевидна.

Рассмотрим случай когда векторы $\vec{a}$ и $\vec{b}$ не коллинеарны.

Отложим от произвольной точки $O$ векторы $\vec{O A} = \vec{a}$ и $\vec{O B} = \vec{b}$ (рис. 3).

Векторы $\vec{O A}$ и $\vec{O B}$ лежат в плоскости $O A B$ . В этой же плоскости лежат векторы $\vec{O A_{1}} = x \cdot \vec{O A}$ и $\vec{O B_{1}} = y \cdot \vec{O B}$ , а значит и их сумма лежит в этой плоскости:

$\vec{c} = \vec{O C} = \vec{O A_{1}} + \vec{O B_{1}} = x \cdot \vec{O A} + y \cdot \vec{O B}$ .

Таким образом векторы $\vec{a}$ , $\vec{b}$ и $\vec{c}$ лежат в одной плоскости, т. е. компланарны.

Теорема доказана.

Из теоремы о разложении вектора по двум неколлинеарным векторам (эта теорема доказывалась в курсе планиметрии) следует и обратное утверждение.

Теорема 2 (обратная признаку компланарности)

Если векторы $\vec{a}$ , $\vec{b}$ и $\vec{c}$ компланарны, а векторы $\vec{a}$ и $\vec{b}$ не коллинеарны, то вектор $\vec{c}$ можно разложить по векторам $\vec{a}$ и $\vec{b}$ , т.е. представить в виде $\vec{с} = x \vec{a} + y \vec{b}$ , причём коэффициенты разложения $x$ и $y$ определяются единственным образом.

Упражнение 1

Дан куб $A B C D A_{1} B_{1} C_{1} D_{1}$ . Определите, являются ли компланарными векторы:

а) $\vec{A B_{1}}$ , $\vec{A D}$ и $\vec{B_{1} D}$ ; б) $\vec{B_{1} C_{1}}$ , $\vec{C_{1} D}$ и $\vec{B_{1} D}$ ;

в) $\vec{A B}$ , $\vec{A D}$ и $\vec{A A_{1}}$ ; г) $\vec{D A}$ , $\vec{D C}$ и $\vec{D B_{1}}$ .

Правило параллелепипеда

Опишем так называемое правило параллелепипеда, которым можно пользоваться при сложении трёх некомпланарных векторов.

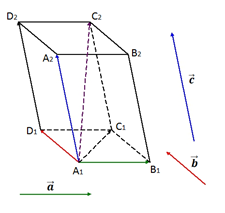Рис. 4. Правило параллелепипеда

Пусть даны некомпланарные векторы $\vec{a}$ , $\vec{b}$ и $\vec{c}$ . От произвольной точки $A_{1}$ отложим векторы $\vec{A_{1} B_{1}} = \vec{a}$ , $\vec{A_{1} D_{1}} = \vec{b}$ , $\vec{A_{1} A_{2}} = \vec{c}$ . Построим параллелепипед $A_{1} B_{1} C_{1} D_{1} A_{2} B_{2} C_{2} D_{2}$ так, чтобы отрезки $A_{1} B_{1},$ $A_{1} D_{1}$ , $A_{1} A_{2}$ были его рёбрами (рис. 4). Тогда вектор $\vec{A_{1} С_{2}}$ является суммой данных векторов $\vec{a}$ , $\vec{b}$ и $\vec{c}$ , т.е. $\vec{A_{1} С_{2}} = \vec{a} + \vec{b} + \vec{c}$ .

Упражнение 2

В кубе $A B C D A_{1} B_{1} C_{1} D_{1}$ найдите вектор, начало и конец которого являются вершины куба, равный сумме векторов:

а) $\vec{C_{1} B_{1}} + \vec{C_{1} D_{1}} + \vec{C_{1} C}$ ; б) $\vec{B A} + \vec{B C} + \vec{B B_{1}}$ ;

в) $\vec{A B} + \vec{A_{1} D_{1}} + \vec{A A_{1}}$ ; г) $\vec{B_{1} A_{1}} + \vec{B C} + \vec{B_{1} B}$ .

Разложение вектора по трём некомпланарным векторам

Представление вектора $\vec{p}$ в виде $\vec{p} = x \vec{a} + y \vec{b} + z \vec{c}$ , где $x$ , $y$ и $z$ – некоторые числа, называют разложением вектора $\vec{p}$ по векторам $\vec{a}$ , $\vec{b}$ и $\vec{c}$ . Числа $x$ , $y$ и $z$ называются коэффициентами разложения.

Сформулируем и докажем теорему о разложении вектора по трём некомпланарным векторам.

Теорема 3

Любой вектор можно разложить по трём данным некомпланарным векторам, причём коэффициенты разложения определяются единственным образом.

Доказательство

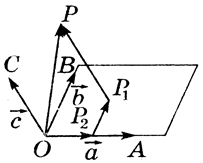Рис. 5. К доказательству теоремы 3

Даны некомпланарные векторы $\vec{a}$ , $\vec{b}$ и $\vec{c}$ . Отложим от произвольной точки $O$ векторы $\vec{O A} = \vec{a}$ , $\vec{O B} = \vec{b}$ , $\vec{O C} = \vec{c}$ , $\vec{O P} = \vec{p}$ (рис. 5).

Проведём через точку $P$ прямую, параллельную прямой $O C$ .

Пусть $P_{1}$ – точка пересечения этой прямой с плоскостью $A O B$ . Через точку $P_{1}$ проведём прямую, параллельную прямой $O B$ .

Пусть $P_{2}$ – точка пересечения этой прямой с прямой $O A$ . Согласно правилу многоугольника

$\vec{O P} = \vec{O P_{2}} + \vec{P_{2} P_{1}} + \vec{P_{1} P}$ ,

$\vec{O P_{2}} ∥ \vec{O A}$ , $\vec{P_{2} P_{1}} ∥ \vec{O B}$ , $\vec{P_{1} P} ∥ \vec{O C}$ . Следовательно, существуют числа $x$ , $y$ и $z$ такие, что $\vec{O P_{2}} = x \cdot \vec{O A}$ , $\vec{P_{2} P_{1}} = y \cdot \vec{O B}$ , $\vec{P_{1} P} = z \cdot \vec{O C}$ .

Таким образом,

$\vec{O P} = x \cdot \vec{O A} + y \cdot \vec{O B} + z \cdot \vec{O C}$

$\vec{p} = x \cdot \vec{a} + y \cdot \vec{b} + z \cdot \vec{c}$ .

Докажем теперь, что коэффициенты разложения определяются единственным образом.

Предположим, что некоторый вектор $\vec{p}$ можно разложить по некомпланарным векторам $\vec{a}$ , $\vec{b}$ и $\vec{c}$ двумя разными способами, т.е. $\vec{p} = x_{1} \cdot \vec{a} + y_{1} \cdot \vec{b} + z_{1} \cdot \vec{c}$ и $\vec{p} = x_{2} \cdot \vec{a} + y_{2} \cdot \vec{b} + z_{2} \cdot \vec{c}$ .

Вычитая из первого равенства второе, получим

$\vec{0} = (x_{1} - x_{2}) \cdot \vec{a} + (y_{1} - y_{2}) \cdot \vec{b} + (z_{1} - z_{2}) \cdot \vec{c}$ .

Так как векторы $\vec{a}$ , $\vec{b}$ и $\vec{c}$ не компланарны, то это равенство возможно только в случае, если $x_{1} - x_{2} = 0$ , $y_{1} - y_{2} = 0$ , $z_{1} - z_{2} = 0$ $\Rightarrow x_{1} = x_{2}$ , $y_{1} = y_{2}$ , $z_{1} = z_{2}$ .

Следовательно, коэффициенты разложения $\vec{p} = x \cdot \vec{a} + y \cdot \vec{b} + z \cdot \vec{c}$ определяются единственным образом.

Теорема доказана.

Упражнение 3

В параллелепипеде $A B C D A_{1} B_{1} C_{1} D_{1}$ разложите:

а) вектор $\vec{A C_{1}}$ по векторам $\vec{A B}$ , $\vec{A D}$ и $\vec{A A_{1}}$ ;

б) вектор $\vec{A A_{1}}$ по векторам $\vec{D_{1} A_{1}}$ , $\vec{D_{1} C_{1}}$ и $\vec{A_{1} C}$ ;

в) вектор $\vec{D_{1} B}$ по векторам $\vec{D_{1} A_{1}}$ , $\vec{D_{1} C_{1}}$ и $\vec{D_{1} D}$ ;

г) вектор $\vec{B B_{1}}$ по векторам $\vec{C B}$ , $\vec{C D}$ и $\vec{B_{1} D}$ .

Контрольные вопросы

Какие векторы называются компланарными?
Сформулируйте признак компланарности трёх векторов.
В чем заключается правило параллелепипеда, используемое при сложении трёх некомпланарных векторов?
Сформулируйте теорему о разложении вектора по трём неколлинеарным векторам.

Ответы

Упражнение 1

а) да; б) да; в) нет; г) нет.

Упражнение 2

а) $\vec{C_{1} A}$ ; б) $\vec{B D_{1}}$ ; в) $\vec{A C_{1}}$ ; г) $B_{1} D$ .

Упражнение 3

а) $\vec{A C_{1}} = \vec{A B} + \vec{A D} + \vec{A A_{1}}$ ;

б) $\vec{A A_{1}} = \vec{D_{1} C_{1}} - \vec{D_{1} A_{1}} - \vec{A_{1} C}$ ;

в) $\vec{D_{1} B} = \vec{D_{1} A_{1}} + \vec{D_{1} C_{1}} + \vec{D_{1} D}$ ;

г) $\vec{B B_{1}} = \vec{C D} - \vec{B_{1} D} - \vec{C B}$ .

Конспект урока: Компланарные векторы. Правило параллелепипеда. Разложение вектора по трём некомпланарным векторам

Другие разделы

Компланарные векторы

Правило параллелепипеда

Разложение вектора по трём некомпланарным векторам